
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Phương pháp : Dãy số giảm bị chặn dưới thì có giới hạn.
Cách giải : Dễ thấy dãy số đã cho là dãy số dương.
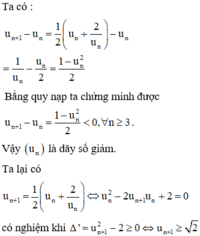
Vậy dãy số đã cho giảm và bị chặn dưới nên có giới hạn.
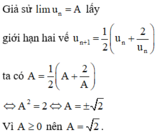

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)

Ta có x n = 1 log n 2010 với n = 2;3;4..
Khi đó
a = x 11 + x 12 + x 13 + x 14 + x 24 = log 2010 11 + log 2010 12 + log 2010 13 + log 2010 14 + log 2010 24 = log 2010 11 . 12 . 13 . 14 . 24 b = x 63 + x 64 + x 65 + x 66 + x 67 = log 2010 63 . 64 . 65 . 66 . 67
Suy ra
b - a = log 2010 2 . 3 . 5 . 6 . 7 = log 2010 2010 = 1
Đáp án B

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

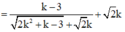

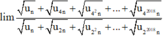
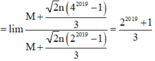 .
.

Suy ra:
a k = a k - 1 + 4 k - 1 + 3 = a k - 2 + 4 k - 2 + 4 k - 1 + 2 . 3 = . . . = a 1 = 4 1 + 2 + . . + k - 1 + 3 k - 1 = 2 k + 3 k - 1
Do đó:
l i m a n + a 4 n + a 4 2 n + . . + a 4 2018 n a n + a 2 n + a 2 2 n + . . + a 2 2018 n
= 1 2 + 4 2 + 4 2 2 + . . + 4 2018 2 1 2 + 2 2 + 2 2 2 + . . + 2 2018 2
= 2 2019 + 1 3
Đáp án C