Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) *Xét ΔABD & ΔEBD
+)AB=BE
+)^ABD=^DBC
+)chung BD
=>ΔABD=ΔEBD(cgc)
b) vì ΔABD=ΔEBD(cmt)
=>^A=^BED(2 góc tg ứng)
=>^BED=90°(^A=90°)
=>DE vg góc vs BC
c) vì ΔBAC vg ở A
=>^BAH+^HAC=90° (1)
Lại có :ΔAHC vg ở H
=>^HAC+^ACB=90° (2)
Từ (1),(2)=>^BAH=^ACB(đpcm)
Ta có :
a) *Xét ΔABD & ΔEBD
+)AB=BE
+)^ABD=^DBC
+)chung BD
=>ΔABD=ΔEBD(cgc)
b) vì ΔABD=ΔEBD(cmt)
=>^A=^BED(2 góc tg ứng)
=>^BED=90°(^A=90°)
=>DE vg góc vs BC
c) vì ΔBAC vg ở A
=>^BAH+^HAC=90° (1)
Lại có :ΔAHC vg ở H
=>^HAC+^ACB=90° (2)
Từ (1),(2)=>^BAH=^ACB(đpcm)

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
mà \(\widehat{BAD}=90^0\)(gt)
nên \(\widehat{BED}=90^0\)(đpcm)

a) Xét tgiac ABD và EBD có:
+ AB = BE
+ BD chung
+ góc ABD = EBD
=> Tgiac ABD = EBD (c-g-c)
=> đpcm
b) Tgiac ABD = EBD (cmt) => AD = DE (hai cạnh t/ứng)
Xét tgiac ADE có AD = DE => Tgiac ADE cân tại D
=> đpcm
c) AH \(\perp\)BC, DE\(\perp\)BC => AH\(//\)DE
=> góc HAE = AED (2 góc SLT do AH\(//\)DE)
Mà tgiac ADE cân tại D (cmt) => góc AED = DAE
=> góc HAE = DAE
=> AE là tia pgiac góc HAC (đpcm)
d) Xét tgiac ADK và EDC có:
+ góc DAK = DEC = 90o
+ góc ADK = EDC (2 góc đối đỉnh)
+ AD = DE (do tgiac ABD = EBD)
=> Tgiac ADK = EDC (g-c-g)
=> AK = EC và KD = DC (2 cạnh t/ứng)
=> Tgiac KDC cân tại K => Góc DCK = (180o- góc KDC) /2
Tgiac AED cân tại D => góc EAD = (180o- góc ADE) /2
Mà góc ADE = KDC (2 góc đối đỉnh) => góc DCK = EAD
Mà 2 góc này SLT => AE \(//\)KC
=> đpcm

a) Xét tam giác BAD và tam giác BED ta có
AB=AD(gt)
góc B1= góc B2 (tia phân giác)
BD chung
tam giác BAD = tam giác BED (c.g.c)
Suy ra: góc A = góc E ( 2 góc tương ứng )
b) Ta có : góc H =E ( =90 độ)
suy ra : AH//DE ( vì AH và DE cùng vuông với BC)
Còn câu c để mình nghĩ lốt nha

`a)`
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
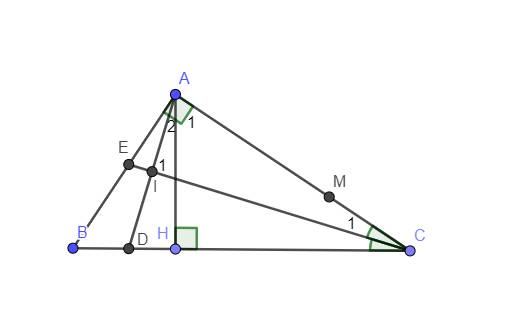

a: ΔBAD cân tại B
=>góc BAD=góc BDA
b: góc BAD+góc CAD=90 độ
góc BDA+góc HAD=90 độ
mà góc BAD=góc BDA
nên góc CAD=góc HAD
=>AD là phân giác của góc HAC
c: Xét ΔABC có AB<AC
nên góc ABC>góc ACB
d: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
=>AH=AK
e: (AB+AC)^2=AB^2+AC^2+2*AB*AC
=BC^2+2*AH*BC<BC^2+2*AH*BC+AH^2=(BC+AH)^2
=>AB+AC<BC+AH

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
Xét tam giác vuông ABHGóc HAB+ góc HBA=90độ(1)
Xét tam giác vuông ABC: góc ABC + góc ACB=90 độ(2)
Từ (1),(2)=> góc HAB = góc HCA