Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác vuông ABD và tam giác HBD có:
BD chung
\(\widehat{ABD=}\widehat{HBD}\)(BD p/g của B)
\(\Rightarrow\)Tam giác HBD=Tam giác ABD(cạnh huyền-góc nhọn)
b,Vì Tam giác HBD=Tam giác ABD(cạnh huyền-góc nhọn)
\(\Rightarrow AD=DH\)
mà DH<DC(vì trong tam giác vuông cạnh góc vuông luôn luôn bé hơn cạnh huyền)
\(\Rightarrow\)AD<DC
c, Ta có AD=DH(câu a) \(\Rightarrow AD^2=DH^2\)
AK=HC(gt) \(\Rightarrow\)\(AK^2=HC^2\)
\(\Rightarrow KD^2=DC^2\Rightarrow KD=DC\)
Vậy tam giác DKC là tam giác cân tại D
Hok tốt

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H co
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: DA=DH
DH<DC
=>DA<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
=>ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC can tại B
mà BI là trung tuyến
nên BI là phân giác của góc KBC
mà BD là phân giác
nên B,D,I thẳng hàng

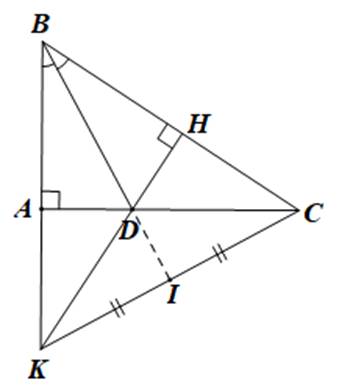
a) Xét \(\Delta\)\(\text{ }\text{ABD}\) và \(\text{ΔHBD}\) có
\(\widehat{\text{BAD}}=\widehat{\text{BHD}}=\text{90}^{\text{o}}\)
\(\text{BD}\) là cạnh chung
\(\widehat{\text{ABD}}=\widehat{\text{HBD}}\) (do \(\text{BD}\) là tia phân giác của \(\widehat{\text{ABD}}\) )
Vậy \(\text{ΔABD = ΔHBD}\) (cạnh huyền – góc nhọn)
___________________________________________________
b) Từ \(\text{ΔABD = ΔHBD}\) (câu a) suy ra\(\text{ AD = HD}\) (hai cạnh tương ứng)
Xét \(\text{ΔDHC}\) vuông tại \(\text{H}\) có \(\text{DC}\) là cạnh huyền nên \(\text{DC}\) là cạnh lớn nhất
Do đó \(\text{DC}\)\(>\text{HD}\) nên \(\text{DC}>AD\)
________________________________________________________
c) Xét \(\text{ΔBKC}\) có \(\text{CA ⊥ BK, KH ⊥ BC}\) và \(\text{CA}\) cắt \(\text{KH}\) tại \(\text{D}\)
Do đó \(\text{D}\) là trực tâm của \(\text{BKC}\), nên \(\text{BD ⊥ KC (1)}\)
Gọi \(\text{J}\) là giao điểm của \(\text{BD và KC}\)
Xét \(\text{ΔBKJ}\) và \(\text{ΔBCJ}\) có
\(\widehat{\text{BJK}}=\widehat{BJC}=90^o\)
\(\text{BJ}\) là cạnh chung
\(\widehat{\text{KBJ}}=\widehat{\text{CBJ}}\) (do \(\text{BJ}\) là tia phân giác của \(\widehat{\text{ABD}}\) )
\(\Rightarrow\) \(\text{ΔBKJ = ΔBCJ}\) (cạnh góc vuông – góc nhọn kề)
Suy ra\(\text{ KJ = CJ}\) (hai cạnh tương ứng)
Hay \(\text{J}\) là trung điểm của \(\text{KC}\)
theo bài ra : \(\text{I}\) là trung điểm của \(\text{KC}\) nên \(\text{I}\) và \(\text{J}\) trùng nhau.
Vậy \(\text{B, D, I}\) thẳng hàng

a) Xét hai tam giác vuông ABD và HBD có: BD là cạnh chung
DA = DH (D nằm trên tia phân giác của góc B)
⇒ΔABD=ΔHBD⇒ΔABD=ΔHBD (cạnh huyền – cạnh góc vuông)
b) Từ câu a) có ΔABD=ΔHBD⇒AB=BHΔABD=ΔHBD⇒AB=BH
Suy ra, ΔBKCΔBKC cân tại B.
Khi đó, BD vừa là phân giác, vừa là đường cao xuất phát từ đỉnh B ⇒D⇒D là trực tâm của ΔBKC.ΔBKC.
Mặt khác, ΔCAK=ΔKHC(c–g–c)ΔCAK=ΔKHC(c–g–c)
⇒KH⊥BC⇒KH⊥BC
⇒⇒ KH là đường cao kẻ từ đỉnh K của .. nên KH phải đi qua trực tâm H.
Vậy ba điểm K, D, H thẳng hàng.

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D