Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)

1.Xét ΔHBA và ΔABC có:
góc AHB=góc BAC=90o
Góc B chung
=> ΔABC đồng dạng ΔHBA (g.g)
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)\(\Rightarrow BA.BA=BH.BC\)
2. Xét ΔHBI và ΔABE có:
góc ABE=IBH (Vì BE là tia phân giác của góc B, I nằm trên BE)
góc BAE=góc IHB=90o
=>ΔHBI đồng dạng ΔABE (g.g)

a.
Xét hai tam giác vuông ABC và HBA có:
\(\left\{{}\begin{matrix}\widehat{HBA}\text{ chung}\\\widehat{BAC}=\widehat{BHA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
b.
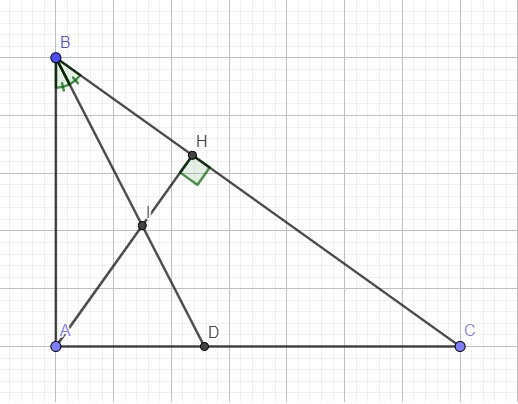
Do BD là phân giác góc B, áp dụng định lý phân giác cho tam giác ABC:
\(\dfrac{AD}{DC}=\dfrac{AB}{BC}\) (1)
Do BI là phân giác góc B, áp dụng định lý phân giác cho tam giác ABH:
\(\dfrac{HI}{AI}=\dfrac{BH}{AB}\) (2)
Mặt khác, từ câu a do \(\Delta ABC\sim\Delta HBA\Rightarrow\dfrac{AB}{BH}=\dfrac{BC}{BA}\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{AB}\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{HI}{IA}=\dfrac{AD}{DC}\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạg với ΔHBA
b: Sửa đề: S ABC/S HBA=25/9
=>AB/HB=BC/BA=AC/HA=5/3
=>15/HB=BC/15=AC/HA=5/3
=>HB=9cm; BC=25cm
AC=căn 25^2-15^2=20cm
AH=15*20/25=12cm

Giải thích các bước giải:
a. N là trung điểm AC; P là trung điểm CH⇒NP là đường trung bình của ΔACH ⇒NP || AH và NP=AH/2
tương tự: MQ là đường trung bình ΔABH ⇒MQ || AH và MQ=AH/2
⇒MQ || NP (cùng || AH)
b. theo câu a⇒NP và MQ ⊥ BC (vì AH ⊥ BC)
M là trung điểm AB, N là trung điểm AC⇒MN là đường trung bình ΔABC
⇒MN || BC và MN=BC/2⇒MN ⊥ MQ và MN ⊥ NP
⇒MNPQ là hình chữ nhật
c. để MNPQ là hình vuông ⇔MN=MQ=NP=QP
mà MQ=AH/2 và MN=BC/2 ⇒AH=BC
a. N là trung điểm AC; P là trung điểm CH⇒NP là đường trung bình của ΔACH ⇒NP || AH và NP=AH/2
tương tự: MQ là đường trung bình ΔABH ⇒MQ || AH và MQ=AH/2
⇒MQ || NP (cùng || AH)
b. theo câu a⇒NP và MQ ⊥ BC (vì AH ⊥ BC)
M là trung điểm AB, N là trung điểm AC⇒MN là đường trung bình ΔABC
⇒MN || BC và MN=BC/2⇒MN ⊥ MQ và MN ⊥ NP
⇒MNPQ là hình chữ nhật
c. để MNPQ là hình vuông ⇔MN=MQ=NP=QP
mà MQ=AH/2 và MN=BC/2 ⇒AH=BC

a, áp dụng đ/lý pytago vào tam giác ABC có A =90 độ
BC^2=AB^2+AC^2
BC^2=6^2+8^2=100
BC=10
b, Xét tam giác ABC và tam giác AHB có
góc BAC=góc BHA=90độ
B góc chung
=> tam giác ABC đồng dạng với tam giác HBA ( gg)
c => AB/HB = BC/BA => AB^2 = HB.BC
a, áp dụng đ/lý pytago vào tam giác ABC có A =90 độ
BC2=AB2+AC2
BC2=62+82=100
BC=10
b, Xét tam giác ABC và tam giác AHB có
góc BAC=góc BHA=90độ
B góc chung
=> tam giác ABC đồng dạng với tam giác HBA ( gg)
c => AB/HB = BC/BA => AB2 = HB.BC
b: Xét ΔABH vuông tại H và ΔCAH vuông tại H có
góc HAB=góc HCA
=>ΔABH đồng dạng vơi ΔCAH