Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) áp dụng định lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
=> 225 = 81 + 144 = 225
=> tam giác ABC là tam giác vuông
trong tam giác vuông ABC có \(\widehat{A}\)> \(\widehat{B}\)>\(\widehat{C}\)(15cm>12cm > 9cm) vì góc đối diện vs cạnh lớn hơn là góc lớn hơn
vậy \(\widehat{A}\)>\(\widehat{B}\)>\(\widehat{C}\)
b) xem lại đề bài
9cm A B C 12cm 15cm D

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

a) Xét tam giác vuông ABC, áp dụng định lý Pi-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC=10\left(cm\right)\)
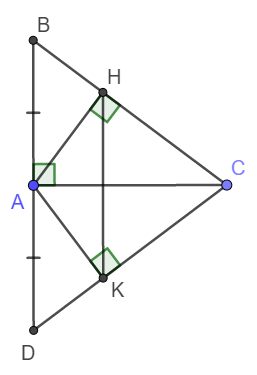
b) Xét tam giác BDC có AC là đường cao đồng thời trung tuyến nên BDC là tam giác cân tại C.
c) Xét tam giác cân BDC có CA là đường cao nên đồng thời là phân giác.
Vậy thì \(\widehat{HCA}=\widehat{KCA}\)
Xét tam giác vuông AHC và tam giác vuông AKC có:
Cạnh huyền AC chung
\(\widehat{HCA}=\widehat{KCA}\)
\(\Rightarrow\Delta AHC=\Delta AKC\) (Cạnh huyền - góc nhọn)
d) Do \(\Delta AHC=\Delta AKC\Rightarrow HC=KC\)
Suy ra tam giác HKC cân tại C. Vậy thì phân giác CA đồng thời là đường cao, hay \(CA\perp HK\)
Lại có \(CA\perp BD\) nên HK // BC.
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Xét ΔABC có AB<AC(9cm<12cm)
mà hình chiếu của AB trên BC là DB
và hình chiếu của AC trên BC là DC
nên BD<DC
b) Xét ΔADB vuông tại D và ΔADN vuông tại D có
DB=DN(gt)
AD chung
Do đó: ΔADB=ΔADN(hai cạnh góc vuông)
Suy ra: AB=AN(Hai cạnh tương ứng)
Xét ΔABN có AB=AN(cmt)
nên ΔABN cân tại A(Định nghĩa tam giác cân)