K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

KV
19 tháng 11 2023
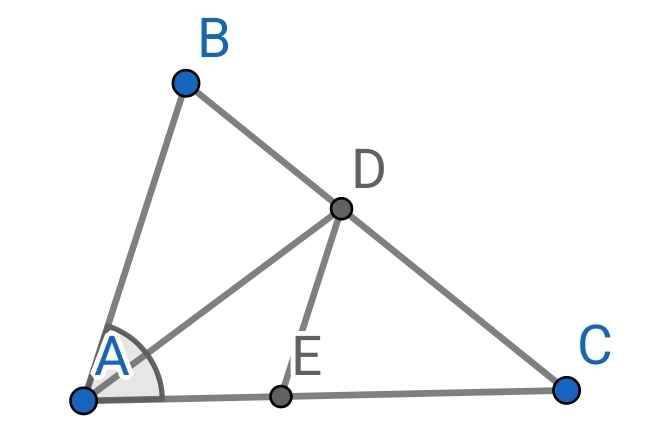 a) Do AD là đường phân giác của ∆ABC (gt)
a) Do AD là đường phân giác của ∆ABC (gt)
⇒ BD/AB = CD/AC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
BD/AB = CD/AC = (BD + CD)/(AB + AC) = BC/(12 + 20) = 28/32 = 7/8
BD/AB = 7/8 ⇒ BD = AB.7/8 = 12.7/8 = 10,5 (cm)
⇒ CD = BC - BD = 28 - 10,5 = 17,5 (cm)
b) ∆ABC có:
DE // AB
⇒ DE/AB = CD/BC
⇒ DE/12 = 17,5/28
⇒ DE = 12 . 17,5/28 = 7,5 (cm)

5 tháng 3 2022
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=8cm\)
Vì BE là pg \(\dfrac{AB}{BC}=\dfrac{AE}{EC}\Rightarrow\dfrac{EC}{BC}=\dfrac{AE}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{EC}{BC}=\dfrac{AE}{AB}=\dfrac{AC}{AB+BC}=\dfrac{8}{16}=\dfrac{1}{2}\Rightarrow EC=5cm;AE=3cm\)









\(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
XétΔABC có BE là phân giác
nên AE/AB=CE/BC
=>AE/5=CE/13
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{5}=\dfrac{CE}{13}=\dfrac{AE+CE}{5+13}=\dfrac{12}{18}=\dfrac{2}{3}\)
Do đó: AE=10/3(cm); CE=26/3(cm)
Áp dụng định lý Pytago cho tam giác ABC:
`AB^2 + AC^2 = BC^2`
`=> 5^2 + 12^2 = BC^2`
`=> BC = 13 cm`.
Áp dụng t/c tia phân giác, ta có:
`(BA)/(AE) = (BC)/(EC) <=> 5/(AE) = (13)/(EC) `
`=> 5EC = 13AE` mà `AE + EC = 12 cm`.
`=> 5AE + 5EC = 60 cm`.
`=> 18AE = 60 cm`
`=> AE = 10/3 cm`
`=> EC = 26/3cm`