Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(I\) là giao điểm của \(AM\) và \(BN\Rightarrow IB=\dfrac{2}{3}BN;IN=\dfrac{1}{3}BN;AI=\dfrac{2}{3}AM;IM=\dfrac{1}{3}AM\)
\(\Delta ANB\) vuông tại \(A:AI^2=IB.IN\) \(\Rightarrow AI^2=\dfrac{2}{3}BN\cdot\dfrac{1}{3}BN=\dfrac{2}{9}BN^2\)
Ta cũng có trong \(\Delta ANB:AB^2=IB.BN\)
\(\Leftrightarrow a^2=\dfrac{2}{3}BN\cdot BN=\dfrac{2}{3}BN^2\Leftrightarrow BN^2=\dfrac{3}{2}a^2\)
Suy ra : \(AI^2=\dfrac{2}{9}BN^2=\dfrac{2}{9}\cdot\dfrac{3}{2}a^2=\dfrac{1}{3}a^2\).
Lại có : \(AI=\dfrac{2}{3}AM\Rightarrow AM^2=\dfrac{9}{4}AI^2=\dfrac{9}{4}\cdot\dfrac{1}{3}a^2=\dfrac{3}{4}a^2\)
\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) của \(\Delta ABC\) vuông tại \(A\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC^2=4AM^2=4\cdot\dfrac{3}{4}a^2=3a^2\)
\(\Rightarrow BC=\sqrt{3a^2}=a\sqrt{3}\)
\(\Delta ABC\) vuông tại \(A\) có : \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{3a^2-a^2}=a\sqrt{2}\)
Vậy : \(AC=a\sqrt{2};BC=a\sqrt{3}\)

a)
Có 2 trung tuyến BN, CM cắt nhau suy ra \(BN\perp AM\)
Gọi G là trọng tâm tam giác ABC, ta có \(BG=\dfrac{2}{3}BN=\dfrac{2}{3}.4=\dfrac{8}{3}\left(cm\right)\)
Trong tam giác ABN vuông tại A, đường cao AG, ta có:
\(AB^2=BG.BN\) (hệ thức lượng)
\(\Rightarrow AB=\sqrt{\dfrac{8}{3}.4}=\dfrac{4\sqrt{6}}{3}\left(cm\right)\)
Tam giác ABN vuông tại A
\(\Rightarrow AN^2=BN^2-AB^2\\ \Rightarrow AN=\sqrt{4^2-\left(\dfrac{4\sqrt{6}}{3}\right)^2}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Mà N là trung điểm AC => AC = \(\dfrac{8\sqrt{3}}{3}\left(cm\right)\)
Áp dụng đl pytago vào tam giác ABC:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{4\sqrt{6}}{3}\right)^2+\left(\dfrac{8\sqrt{3}}{3}\right)^2}=4\sqrt{2}\left(cm\right)\)
Thừa dữ kiện AM = 3cm, bạn coi kỹ đề đủ/ đúng hết chưa thì cmt để chút mình coi lại bài giải

bài 1) dùng tỉ số lượng giác lần lượt tính được AD=\(10\sqrt{3}cm\);AC=\(20\sqrt{3}cm\);AB=20cm
do đó Shình thang=\(\frac{\left(AB+CD\right)\cdot AD}{2}=\frac{\left(20+30\right)\cdot10\sqrt{3}}{2}=\frac{500\sqrt{3}}{2}cm^2\)

Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
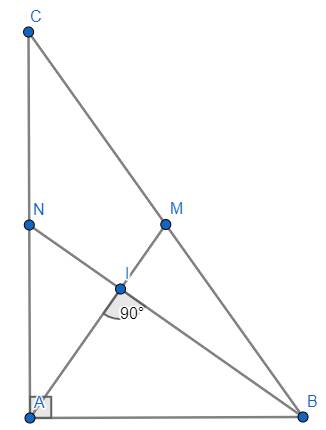
gọi I là trọng tâm của tam giác ABC ta có AI vuông góc với BI
dễ thấy \(AB^2=BI\cdot BN\)
mà \(BI=\frac{2}{3}BN\)(I là trọng tâm)
\(\Rightarrow a^2=\frac{2}{3}BN^2\)
dễ thấy \(AN^2=IN\cdot BN=\frac{1}{3}BN\cdot BN=\frac{1}{3}BN^2=\frac{a^2}{2}\)
suy ra \(AC=\sqrt{2}a\)
\(BC^2=AB^2+AC^2=a^2+2a^2=3a^2\Rightarrow BC=\sqrt{3}a\)