Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
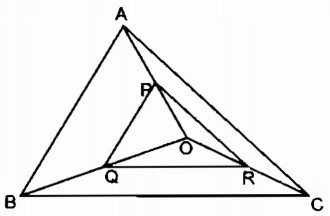
a. Trong tam giác AOB, ta có:
P trung điểm của OA (gt)
Q trung điểm của OB (gt)
Suy ra: PQ là đường trung bình của ∆ OAB.
Suy ra: PQ=12ABPQ=12AB
(tính chất đường trung bình của tam giác )
Suy ra: PQAB=12PQAB=12 (1)
Trong tam giác OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra: PR là đường trung bình của tam giác OAC.
Suy ra: PR=12ACPR=12AC (tính chất đường trung bình của tam giác )
Suy ra: PRAC=12PRAC=12 (2)
Trong tam giác OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra: QR là đường trung bình của tam giác OBC.
Suy ra: QR=12BCQR=12BC (tính chất đường trung bình của tam giác )
Suy ra: QRBC=12QRBC=12 (3)
Từ (1), (2) và (3) suy ra: PQAB=PRAC=QRBC=12PQAB=PRAC=QRBC=12
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c)
b. Gọi p’ là chu vi tam giác PQR.
Ta có: PQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′pPQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′p
Vậy: p′p=12⇒p′=12p=12.543=271,5p′p=12⇒p′=12p=12.543=271,5 (cm)

a,Ta có : ABC^+BAC^+BCA^=180* ( đl tổng 3 góc )
=> 90*+BAC^+30*=180*
=>BAC^=180*-120*=60*
Do AM là tia p/g của BAC^
=> BAM^=MAN^=60*/2=30*
Xét tam giác vuông ABM và tam giác vuông ANM
AM cạnh chung
BAM^=MAN^
=>tam giác ABM = tam giác ANM ( ch-gn )
=>AB=AN (2 cạnh tương ứng)
b,Xét tam giác vuông IBM và tam giác vuông CNM
BMI^=NMC^ ( đối đỉnh )
BM = NM ( cm câu a )
=> tam giác IBM = tam giác CNM ( cgv-gn )
c, Ta có : BMI^ + MBI^ + BIM ^ = 180*
=>BMI^ + 90* + 30* = 180*
=> BMI^=180*-120*=60*
Do BMI^=CMN^
=>BMI^=CMN^=60*
Lại có IMN^=180* ( góc bẹt )
Mà : IMC^+CMN^=180*
=>IMC^=180*-60*=120*
Mặt khác : IM=MC (cm câu b)
=> tam giác IMC cân tại M
=>MIC^=MCI^
dễ thấy : IMC^+MIC^+MCI^=180*
=>MIC^+MCi^=180*-120*=60*
do :MIC^=MCI^
=>MIC^=MCI^=60*/2=30*
Ta có :+)AIC^=BIM^+CIM^=30*+30*=60*
+)ACI^=NCM^+MCI^=30*+30*=60*
+)IAC^=60*
=>tam giác IAC là tam giác đều

Hướng dẫn thôi nhé ^^ toán hình mà chép lời giải thôi thì mất thú vị ^^
Ý a em tính góc EAC (góc kề bù) , tính góc ACE (so le trong)
Ý b dùng định lý tổng 3 góc của tam giác nhé
Còn ý c dùng định lý 1 về quan hệ giữa góc và cạnh dối diện nhé ^^ có gì k hiểu thì ib hỏi chị

Vì AD //CE
=> CAD = ACE = 50°( so le trong )
Mà CAB + CAE = 180°
=> EAC = 50°
=> EAC = ECA = 50°
=> ∆EAC cân tại E
b) Vì EAC + ECA +AEC = 180°
=> AEC = 80°
c) Vì ∆AEC cân tại E
=> AE = EC
Mà EAC = ECA =50°
=> EAC< AED
=> BC là cạnh lớn nhất

a, Vì diện tích tam giác không đổi nên a.ha=b.hb=c.hc. Vì ha=hb=hc nên a=b=c
b, Dùng Pytago: Gọi x là độ dài các cạnh, M là trung điểm BC suy ra MB=x:2,
AB2+BM2AH2 suy ra x2+x2/4=a2.3/4 suy ra x=a
a,
\(\Delta ABC=\Delta PQR\\ \Rightarrow\widehat{A}=\widehat{P}=50^o\\ \widehat{B}=\widehat{Q}\)
Xét \(ABC\) có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=130^o\\ \Rightarrow\widehat{B}=130^o-\widehat{C}\)
\(\widehat{B}-\widehat{C}=50^o\\ \Rightarrow130^o-2\widehat{C}=50^o\\ \Rightarrow\widehat{C}-40^o\\ \Rightarrow\widehat{B}=90^o=\widehat{Q}\)
\(\Rightarrow PQR\) là tam giác vuông
b, \(\Delta ABC=\Delta PQR\\ \Rightarrow\left\{{}\begin{matrix}AC=PR\\AB=PQ\\BC=QR\end{matrix}\right.\)