Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=7\)
Diện tích:
\(S_{ABC}=\dfrac{1}{2}ac.sinB=10\sqrt{3}\)

\(\widehat{B}=180^o-60^o-45^o=75^o\)
Theo định lý sin ta có:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{AB\cdot sinB}{sinC}=\dfrac{5\cdot sin75^o}{sin45^o}=\dfrac{5+5\sqrt{3}}{2}\)
Mà: \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot5\cdot\dfrac{5+5\sqrt{3}}{2}\cdot sin60^o=\dfrac{75+25\sqrt{3}}{8}\left(dvdt\right)\)

Câu 1: Diện tích tam giác là: \(\frac{h_A.a}{2}=\frac{3.6}{2}=9\)(đvdt)
Câu 2: Diện tích tam giác là: \(\frac{1}{2}ab.\sin C=\frac{1}{2}.4.5.\sin60^o=5\sqrt{3}\)(đvdt)
Câu 2: Ta có: \(\hept{\begin{cases}c^2=a^2+b^2-2ab.\cos C\\a^2+b^2>c^2\end{cases}\Rightarrow c^2>c^2-2ab.\cos C\Leftrightarrow2ab.\cos C>0}\)
\(\Rightarrow\cos C>0\Rightarrow C< 90^o\)
Vậy C là góc nhọn

\(p=\dfrac{a+b+c}{2}=15\)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{15\left(15-8\right)\left(15-10\right)\left(15-12\right)}=15\sqrt{7}\)
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{10^2+12^2-8^2}{2.10.12}=\dfrac{3}{4}\Rightarrow A\approx41^024'\)

Tham khảo:
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
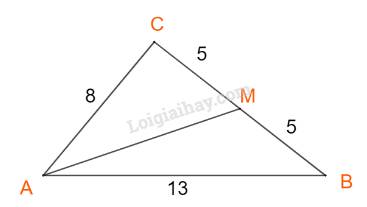
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)

Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)
a, Kẻ \(CH\perp AB\Rightarrow CH=AC.sin60^o=\dfrac{8.\sqrt{3}}{2}=4\sqrt{3}\)
\(\Rightarrow BC=\dfrac{CH}{sin45^o}=\dfrac{4\sqrt{3}}{\dfrac{\sqrt{2}}{2}}=4\sqrt{6}\)
\(AH=AC.cosA=8.cos60^o=4\)
\(BH=\dfrac{CH}{tan45^o}=4\sqrt{3}\)
\(\Rightarrow AB=AH+BH=4\sqrt{3}+4\)
\(\widehat{C}=180^o-\widehat{A}-\widehat{B}=180^o-60^o-45^o=75^o\)
b, \(S_{ABC}=\dfrac{1}{2}.AC.AB.sinA=\dfrac{1}{2}.8.\left(4+4\sqrt{3}\right).sin60^o=24+8\sqrt{3}\)
a) \(\widehat{C}\)= 180-(60+45)=75o