Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tự kẻ hình nha
b) vì AD cắt BE tại G mà AD và BE là trung tuyến=> G là trọng tâm của tam giác ABC=> AG=2/3AD
a)vì G là trong tâm
=> AG=2/3AD=> GD=1/2AG
vì I là trung điểm của AG=> IG=1/2AG
=> BG=2/3BE=> GE=1/2BG
vì K là trung điểm của BG=> KG=1/2BG
xét tam giác GIK và tam gáic GDE có
IG=GD(=1/2AG)
KG=EG(=1/2BG)
IGK=EGD( đối đỉnh)
=> tam giác GIK= tam giác GDE( cgc)
=> IK=ED( hai cạnh tương ứng)
=> KIG=GDE( hai góc tương ứng)
mà KIG so le trong với GDE=> IK//ED


Giải
a) Áp dụng kết quả của bài 64 chương II sách bài tập toán 7 vào ∆ABC và ∆AGB ta có:
DE // AB và DE=1/2AB (1)
IK // AB và IK=1/2AB (2)
Từ (1) và (2) suy ra: DE // IK và DE = IK
b) AD và BE là 2 đường trung tuyến của ∆ABC cắt nhau tại G.
⇒AG=2/3AD(tính chất đường trung tuyến)
Bài này dễ mà
Sử dụng tính chất đường trung tuyến của tam giác rồi CM tam giác IGK = tam giác DGE
=> IK=DE ( 2 cạnh tương ưng )
=> GIK = GDE ( 2 góc tương ứng)
Mà GIK và GDE là 2 góc so le trong
=> ....... (các bạn tự Cm nhé, Mình chỉ gợi ý như thế thôi )

a: Xét ΔABC có
D là trung điểm của BC
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//AB và DE=AB/2(1)
Xét ΔGAB có
I là trung điểm của GA
K là trung điểm của GB
Do đó: IK là đường trung bình
=>IK//AB và IK=AB/2(2)
Từ (1) và (2) suy ra DE//IK và DE=IK
b: Xét ΔABC có
AD là đường trung tuyến
BE là đường trung tuyến
AD cắt BE tại G
Do đó: G là trọng tâm của ΔABC
=>AG=2/3AD

a) Áp dụng kết quả của bài 64 chương II sách bài tập toán 7 tập 1 vào \(\Delta ABC\) và vào \(\Delta AGB\) ta được:
+) \(DE\) // \(AB\) và \(DE=\frac{1}{2}AB\) (1).
+) \(IK\) // \(AB\) và \(IK=\frac{1}{2}AB\) (2).
Từ (1) và (2) => \(DE\) // \(IK\) và \(DE=IK.\)
b) Vì \(AD\) và \(BE\) là 2 đường trung tuyến của \(\Delta ABC\) cắt nhau tại G (gt).
=> \(AG=\frac{2}{3}AD\) (tính chất ba đường trung tuyến của tam giác) (đpcm).
Chúc bạn học tốt!

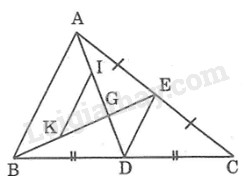
G A B C D E I K
Giải:
a) Ta có: \(AG=\frac{2}{3}AD\Rightarrow\frac{1}{2}AG=\frac{1}{2}.\frac{2}{3}AD\Rightarrow IG=\frac{1}{3}AD\)
\(GD=\frac{1}{3}AD\) ( tính chất đường trung tuyến )
\(\Rightarrow IG=GD\)
\(GB=\frac{2}{3}BE\Rightarrow\frac{1}{2}GB=\frac{1}{2}.\frac{2}{3}BE\Rightarrow KG=\frac{1}{3}BE\)
\(GE=\frac{1}{3}BE\) ( tính chất đường trung tuyến )
\(\Rightarrow GE=KG\)
Xét \(\Delta IKG,\Delta DEG\) có:
IG = GD ( cmt )
\(\widehat{IGK}=\widehat{EGD}\) ( đối đỉnh )
\(GK=GE\) ( cmt )
\(\Rightarrow\Delta IKG=\Delta DEG\left(c-g-c\right)\)
\(\Rightarrow IK=DE\) (
\(\Rightarrow\widehat{IKG}=\widehat{GED}\) ( góc t/ứng ) ( đpcm )
Mà 2 góc trên ở vị trí so le trong
\(\Rightarrow\)IK // DE ( đpcm )
b) Theo tính chất đường trung tuyến
\(\Rightarrow AG=\frac{2}{3}AD\left(đpcm\right)\)
Vậy...