Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a)\) Ta có :
\(\frac{x}{18}=\frac{y}{9}\)\(\Leftrightarrow\)\(\frac{x}{2}=y\)
\(\Rightarrow\)\(x=2y\)
Thay \(x=2y\) vào \(A=\frac{2x-3y}{2x+3y}\) ta được :
\(A=\frac{2.2y-3y}{2.2y+3y}=\frac{4y-3y}{4y+3y}=\frac{y}{7y}=\frac{1}{7}\)
Vậy ... ( tự kết luận )
Chúc bạn học tốt ~

A + B - C = \(x^2-2x\)\(+3xy^2-x^2y+x^2y^2\)\(+\left(-2x^2\right)+3y^2-5x+y+3\)\(-\left(3x^2-2xy+7y^2-3x-5y-6\right)\)
= \(x^2-2x+3xy^2-x^2y+x^2y^2-2x^2+3y^2-5x+y+3-3x^2+2xy-7y^2+3x+5y+6\)
= \(-4x^2+3xy^2-4x-4y^2+6y+2xy+9\)
A-B+C=\(x^2-2x+3xy^2-x^2y+x^2y^2\)\(-\left(-2x^2+3y^2-5x+y+3\right)\)\(+3x^2-2xy+7y^2-3x-5y-6\)
= \(x^2-2x+3xy^2-x^2y+x^2y^2+2x^2-3y^2+5x-y-3\)\(+3x^2-2xy+7y^2-3x-5y-6\)
= \(6x^2+3xy^2+4y^2-2xy-6y-9\)
-A+B+C =\(-\left(x^2-2x+3xy^2-x^2y+x^2y^2\right)\)\(-2x^2+3y^2-5x+y+3+3x^2-2xy+7y^2\)\(-3x-5y-6\)
= \(-x^2+2x-3xy^2+x^2y-x^2y^2\)\(-2x^2+3y^2-5x+y+3\)\(+3x^2-2xy+7y^2-3x-5y-6\)
= \(-6x+10y^2-3xy^2-4y-2xy-3\)
còn bậc cậu tự tìm nha bậc để mà

Lời giải
Có hai cách trình bày với bài này: một là bạn có thể liệt kê hết các phần tử ra hoặc bạn sắp xếp theo cùng thứ tự và tính như sau:
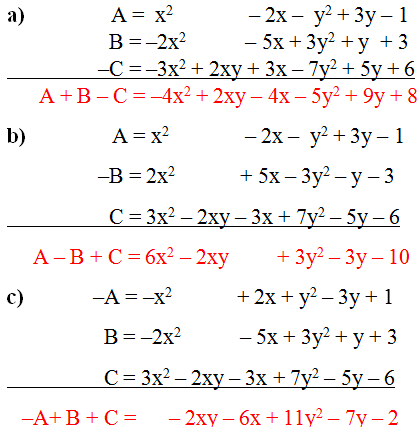
a, \(A+B=x^2-2x-y^2+3y-1+\left(-2x^2+3y^2-5z+3\right)\)
\(=x^2-2x-y^2+3y-1-2x^2+3y^2-5z+3\)
\(=-x^2-2x+2y^2+3y-5z+2\)
b, \(A-B=x^2-2x-y^2+3y-1-\left(-2x^2+3y^2-5z+3\right)\)
\(=x^2-2x-y^2+3y-1+2x^2-3y^2+5z-3\)
\(=3x^2-2x-4y^2+3y+5z-4\)
c, Thay x=-2,y=1 vào biểu thức A-B ta được:
\(A-B=3.\left(-2\right)^2-2.\left(-2\right)-4.1^2+3.1+5z-4=12+4-4+3+5z-4=11+5z\)
\(A=x^2-2x-y^2+3y-1\)
\(B=-2x^2+3y^2-5z+3\)
a) A+B =
\(\left(x^2-2x-y^2+3y-1\right)+\left(-2x^2+3y^2-5z+3\right)\)
\(=\left(x^2-2x^2\right)-\left(y^2+3y^2\right)-2x+3y-5z-1+3\)
\(=-x^2-4y^2-2x+3y-5z-1+3\)
\(=\left(-1-4-2+3-5-1+3\right).\left(x^2-x\right).y^2.z\)
\(=-7xy^2z\)
b ) Tính A-B ( tương tự A+B )
C) Thay x=-2 và y=1 vào biểu thức ta có :
\(-7xy^2z\)
\(=-7.-2.1.z\)
\(=14z\)