Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thực hiện khai triển và rút gọn thu được:
\(B=\frac{x^3}{2}-\frac{1}{2}x^4+\frac{1}{2}x^2+\frac{1}{2}x^4-x^2\)
\(=\frac{x^3}{2}-\frac{x^2}{2}\)
a) Từ biểu thức rút gọn trên suy ra bậc của B(x) là $3$
b) \(B(\frac{1}{2})=\frac{\frac{1}{2^3}}{2}-\frac{(\frac{1}{2})^2}{2}=-\frac{1}{16}\)
c) \(B=\frac{x^3}{2}-\frac{x^2}{2}=\frac{x^2(x-1)}{2}=\frac{x.x(x-1)}{2}\)
Vì \(x(x-1)\) là tích 2 số nguyên liên tiếp nên \(x(x-1)\vdots 2\)
\(\Rightarrow \frac{x(x-1)}{2}\in\mathbb{Z}\)
\(\Rightarrow B=x.\frac{x(x-1)}{2}\in\mathbb{Z}\)
Ta có đpcm.

a) \(x^2y^2-x^2+\left(\dfrac{1}{2}\right)^6x=x^2y^2-x^2+\dfrac{1}{64}x\)
\(\Rightarrow\) đa thức bậc 4
b) \(\left(-9x^2\right)\dfrac{1}{3}y+y\left(-x^2\right)+24x\left(\dfrac{-1}{4}xy\right)\)
\(=-3x^2y-x^2y-6x^2y\)
\(=-10x^2y\)
Thay \(x=1;y=-1\) vào đa thức ta có:
\(-10x^2y=-10.1^2.\left(-1\right)=10\)

a: Đặt A=0
=>-2/3x=5/9
hay x=-5/6
b: Đặt B(x)=0
=>(x-2/5)(x+2/5)=0
=>x=2/5 hoặc x=-2/5
c: Đặt C(X)=0
\(\Leftrightarrow x^3\cdot\dfrac{1}{2}=-\dfrac{4}{27}\)
\(\Leftrightarrow x^3=-\dfrac{8}{27}\)
hay x=-2/3

a)P(x)=\(x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
=\(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Q(x)=\(5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
=\(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
b) P(x)=\(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
+ Q(x)=\(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
__________________________________
P(x)+Q(x)= \(12x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
P(x)=\(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
- Q(x)=\(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
_________________________________________
P(x)-Q(x)=\(2x^5+2x^4-7x^3-6x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
c)Thay x=0 vào đa thức P(x), ta có:
P(x)=\(0^5+7\cdot0^4-9\cdot0^3-2\cdot0^2-\dfrac{1}{4}\cdot0\)
=0+0-0-0-0
=0
Vậy x=0 là nghiệm của đa thức P(x).
Thay x=0 vào đa thức Q(x), ta có:
Q(x)=\(-0^5+5\cdot0^4-2\cdot0^3+4\cdot0^2-\dfrac{1}{4}\)
=0+0-0+0-\(\dfrac{1}{4}\)
=0-\(\dfrac{1}{4}\)
=\(\dfrac{-1}{4}\)
Vậy x=0 không phải là nghiệm của đa thức Q(x).
a) Sắp xếp theo lũy thừa giảm dần
P(x)=x5−3x2+7x4−9x3+x2−14xP(x)=x5−3x2+7x4−9x3+x2−14x
=x5+7x4−9x3−2x2−14x=x5+7x4−9x3−2x2−14x
Q(x)=5x4−x5+x2−2x3+3x2−

Ta có: P(x) = -5x3 - 1313 + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 - 2323.
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:
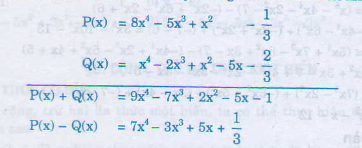 .
.
Ta có: P(x) = -5x3 – 1/3 + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 – 2/3.
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:


\(\dfrac{1}{R\left(x\right)}=\dfrac{1}{x\left(x+2\right)}=\dfrac{1}{2}\left(\dfrac{1}{x}-\dfrac{1}{x+2}\right)\)
\(\Rightarrow S=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2022}-\dfrac{1}{2024}+\dfrac{1}{2023}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{2024}-\dfrac{1}{2025}\right)+\dfrac{1}{2.2023}\)
Một kết quả rất xấu


Nhiều nick nhỉ! :)
ai giúp cho 10 like