Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phần tử không gian mẫu:![]() .
.
(chọn 3 đỉnh bất kì từ 12 đỉnh của đa giác ta được một tam giác)
Gọi A: 3 đỉnh được chọn tạo thành tam giác đều ”.
(Chia 12 đỉnh thành 3 phần. Mỗi phần gồm 4 đỉnh liên tiếp nhau. Mỗi đỉnh của tam giác đều ứng với một phần ở trên.Chỉ cần chọn 1 đỉnh thì 2 đỉnh còn lại xác định là duy nhất).
Ta có: ![]() .
.
Khi đó: 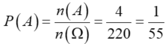 .
.
Chọn A.

S A B C D H M N K
Kẻ \(AH\perp BD\Rightarrow BD\perp\left(SAH\right)\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và (ABCD)
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AB^2}\Rightarrow AH=\frac{AB.AD}{\sqrt{AB^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
\(SA=\sqrt{SD^2-AD^2}=2a\)
\(tan\widehat{SHA}=\frac{SA}{AH}=\frac{4\sqrt{3}}{3}\Rightarrow\widehat{SHA}\simeq66^035'\)
b/ \(MS=MA\Rightarrow d\left(S;\left(MND\right)\right)=d\left(A;\left(MND\right)\right)\)
Từ A kẻ \(AK\perp MD\Rightarrow AK\perp\left(MND\right)\Rightarrow AK=d\left(A;\left(MND\right)\right)\)
\(AM=\frac{SA}{2}=a\Rightarrow\frac{1}{AK^2}=\frac{1}{AM^2}+\frac{1}{AD^2}\Rightarrow AK=\frac{AM.AD}{\sqrt{AM^2+AD^2}}=\frac{a\sqrt{3}}{2}\)

Không gian mẫu: \(n\left(\Omega\right)=C_{16}^3=560\)
Gọi O là tâm (H), chọn 2 đỉnh của (H) sao cho đoạn thẳng nối chúng đi qua O có 8 cách chọn (1)
Với mỗi đỉnh còn lại của (H), chúng sẽ cùng với hai điểm ở (1) tạo thành một tam giác vuông \(\Rightarrow\) còn lại 14 đỉnh
\(\Rightarrow\) có \(14.8=112\) tam giác vuông
Xác suất: \(P=\dfrac{112}{560}=\dfrac{1}{5}\)

Số có 4 chữ số có dạng ![]()
Số phần tử của không gian mẫu: n(S)=9.9.8.7=4536.
Gọi A: “ tập hợp các số tự nhiên có 4 chữ số phân biệt và lớn hơn 2500.”
TH1: a>2
Chọn a: có 7 cách chọn.
Chọn b: có 9 cách chọn.
Chọn c: có 8 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có:7.9.8.7=3528 .
TH2: a=3; b>5
Chọn a: có 1 cách chọn.
Chọn b: có 4 cách chọn.
Chọn c: có 8cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.4.8.7=224 (số).
TH3: a=2; b=5; c>0
Chọn a: có 1 cách chọn.
Chọn b: có1 cách chọn.
Chọn c: có 7 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.7.7=49(số).
TH4. a=2; b=5; c=0 ;d>0
Chọn a: có 1 cách chọn.
Chọn b: có 1 cách chọn.
Chọn c: có 1 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.1.7=7(số).
Như vậy: n(A)=3528+224+49+7=3808
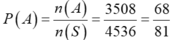
Chọn C.
Đáp án D
Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2 .