Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Có AB = AC (gt)
BD = CE (gt)
--> AB + BD = AC + CE
--> AD = AE
Xét tam giác ADC và tam giác AEB, có
AC = AB
^DAC = ^EAB
AD = AE (cmt)
--> tg ADC = tg AEB ( c.g.c(
--> ^D = ^E
^ACD = ^ABE
--> 180 độ - ^ACD = 180 độ - ^ABE
--> ^ICE = ^ IBD
Tự CM tg IBD = tg ICE ( g. c .g )
--> IB = IC, ID = IE
b) Xét tg IBC và tg IED
2 tg = nhau theo TH (c.g.c)
--> ^CBI = ^DEI
2 góc này ở vị trí SLT
--> BC // DE
c) Xét tg ABI và tg ACI, có
AB = AC (gt)
Chung AI
BI = IC (cmt)
--> tg ABI = tg ACI --> ^BAI = ^CAI
--> AI là p/g ^BAC
CMTT --> AM cũng là p/g ^BAC
--> A, I, M thẳng hàng. <3

)BD=CE mà AB=AC -> EA=DA
a) xét tam giác EAB và tam giác DAC có :
AB=AC ( tam giác ABC cân tại A )
góc EAB = góc DAC (đối đỉnh )
EA=AD (cmt)
-> tam giác EAB=tam giác DAC ( c.g.c)
-> góc EBA = góc DCA ( cặp góc tương ứng )
-> ED=DC ( cặp cạnh tương ứng )
*) tam giác ABC cân tại A -> góc B = góc C
mà góc EBA=góc DCA -> góc EBC= góc DCB
-> tan giác IBC cân tại I -> IB=IC
**) IB=IC ( cmt )
mà EB=DC
-> ID=IE
b) tam giác AED có AE=AD
-> tam giác AED cân tại A -> góc AED = góc EDA (1)
góc B = góc C (cmt) (2)
góc EAD = góc BAC ( đối đỉnh ) (3)
từ (1), (2), (3) -> góc AED = góc ACB
mà 2 góc ở vị trí so le trong -> ED//BC
c) ED cắt IA tại H
xét tam giác IEA và tam giác IDA (cm tương tự ) 2 tam giác = nhau theo trường hợp cạnh góc cạnh
-> I,H,A thẳng hàng (4)
vì ED//BC .
M là trung điểm của BC -> M cũng là trung điểm của ED
-> H , A , M thằng hàng (5)
từ (4) và (5) -> I ,A,M thẳng hàng
)BD=CE mà AB=AC -> EA=DA
a) xét tam giác EAB và tam giác DAC có :
AB=AC ( tam giác ABC cân tại A )
góc EAB = góc DAC (đối đỉnh )
EA=AD (cmt)
-> tam giác EAB=tam giác DAC ( c.g.c)
-> góc EBA = góc DCA ( cặp góc tương ứng )
-> ED=DC ( cặp cạnh tương ứng )
*) tam giác ABC cân tại A -> góc B = góc C
mà góc EBA=góc DCA -> góc EBC= góc DCB
-> tan giác IBC cân tại I -> IB=IC
**) IB=IC ( cmt )
mà EB=DC
-> ID=IE
b) tam giác AED có AE=AD
-> tam giác AED cân tại A -> góc AED = góc EDA (1)
góc B = góc C (cmt) (2)
góc EAD = góc BAC ( đối đỉnh ) (3)
từ (1), (2), (3) -> góc AED = góc ACB
mà 2 góc ở vị trí so le trong -> ED//BC
c) ED cắt IA tại H
xét tam giác IEA và tam giác IDA (cm tương tự ) 2 tam giác = nhau theo trường hợp cạnh góc cạnh
-> I,H,A thẳng hàng (4)
vì ED//BC .
M là trung điểm của BC -> M cũng là trung điểm của ED
-> H , A , M thằng hàng (5)
từ (4) và (5) -> I ,A,M thẳng hàng
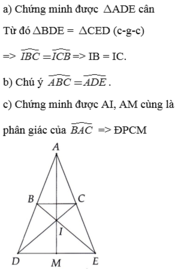
a, Xét tam giác BEC và tam giác CDB có :
\(\left\{{}\begin{matrix}CE=BD\left(gt\right)\\\widehat{BCE}=\widehat{CBD}\left(kềbùvớihaigócbằngnhau\widehat{ABC}=\widehat{ACB}\right)\\BClàcạnhchung\end{matrix}\right.\\ \Rightarrow\Delta BCE=\Delta CBD\left(c-g-c\right)\\ \Rightarrow\widehat{CBE}=\widehat{BCD}\left(haigóctươngứng\right)\)
và \(\Rightarrow\widehat{BDE}=\widehat{CED}\left(haigóctươngứng\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\Delta BICcântạiI\\\Delta DIEcântạiI\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}IB=IC\\ID=IE\end{matrix}\right.\)
b, Xét 2 tam giác cân BIC và DIE có :
\(\left\{{}\begin{matrix}\widehat{CBI}+\widehat{BCI}+\widehat{BIC}=180^0\\\widehat{DEI}+\widehat{IDE}+\widehat{DIE}=180^0\end{matrix}\right.\)
Ta có : \(\widehat{BIC}=\widehat{DIE}\)( hai góc đối đỉnh )
\(\Rightarrow\widehat{CBI}+\widehat{BCI}=\widehat{DEI}+\widehat{IDE}\)
Mà : \(\widehat{CBI}=\widehat{BCI};\widehat{DEI}=\widehat{IDE}\)
\(\Rightarrow\widehat{CBI}=\widehat{BCI}=\widehat{DEI}=\widehat{IDE}\)
\(\Rightarrow BC//DE\)( vì góc BCD và góc CDE nằm ở vị trí so le trong )
c, Xét tam giác ABM và tam giác ACM có :
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\AMlàcạnhchung\\BM=MC\left(gt\right)\end{matrix}\right.\\ \Rightarrow\Delta ABM=\Delta ACM\left(c-c-c\right)\\ \Rightarrow\widehat{BAM}=\widehat{CAM}\left(haigóctươngứng\right)\)
\(\Rightarrow\) AM là tia phân giác của góc BAC (1)
Xét tam giác ABI và tam giác ACI có :
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\AIlàcạnhchung\\BI=MI\left(cmt\right)\end{matrix}\right.\\ \Rightarrow\Delta ABI=\Delta ACI\left(c-c-c\right)\\ \Rightarrow\widehat{BAI}=\widehat{CAI}\left(haigóctươngứng\right)\)
\(\Rightarrow\)AI là tia phân giác của góc BAC (2)
Từ (1) và (2) ta có :
AI trùng với AM ( vì cùng là tia phân giác góc BAC)
\(\Rightarrow\) A, M, I thẳng hàng.