Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM vừa là đường phân giác vừa là đường cao
b: Xét ΔABC có
AM là đường trung tuyến
AO=2/3AM
Do đó: O là trọng tâm của ΔABC
=>BO là đường trung tuyến ứng với cạnh AC
hay E là trung điểm của AC
c: Ta có: O là trọng tâm của ΔABC
mà CO cắt BA tại F
nên F là trung điểm của AB
Xét ΔABE và ΔACF có
AB=AC
\(\widehat{BAE}\) chung
AE=AF
Do đó: ΔABE=ΔACF
Suy ra: BE=CF

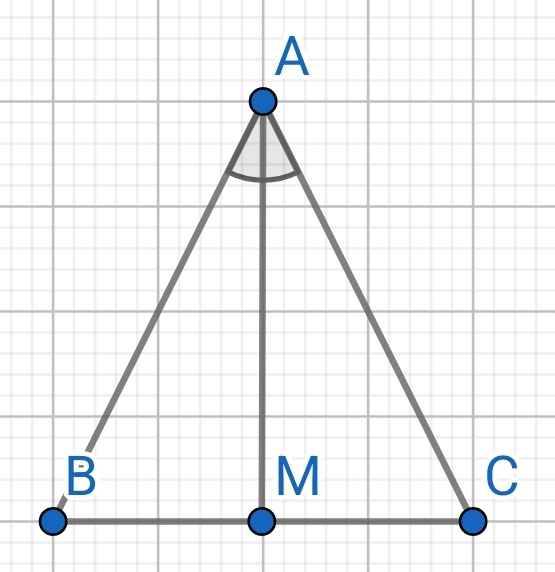
a: ΔABC cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
b: Xét ΔABC có
M là trung điểm của BC
MN//AB
=>N là trung điểm của AC
ΔAMC vuông taij M
mà MN là trung tuyến
nên MN=NA
c: Xét ΔABC có
BN.AM là trung tuyến
BN cắt AM tại O
=>O là trọng tâm

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔABH=ΔACH
b: góc DAH=góc HAC=góc DHA
=>ΔDAH cân tại D
=>góc DHB=góc DBH
=>DH=DB=DA
=>D là trung điểm của AB
=>DH=1/2AB


Mình chỉ biết làm phần a, và b, thôi. Mong bạn thông cảm
\(a,\text{Ta có: M là trung điểm của BC}\Rightarrow BM=CM\)
\(\text{Xét }\Delta MHB\text{ và }\Delta MKCcó:\)
\(MH=MK\left(gt\right)\left(1\right)\)
\(\widehat{HMB}=\widehat{KMC}\left(\text{đối đỉnh}\right)\left(2\right)\)
\(BM=CM\left(cmt\right)\left(3\right)\)
\(\text{Từ (1), (2) và (3)}\Rightarrow\Delta MHB=\Delta MKC\left(c.g.c\right)\left(đpcm\right)\)
\(b,\text{Do }MH\perp AB\left(gt\right)\Rightarrow\widehat{BHM}=\widehat{AHM}=90^o\)
\(\text{Do }\Delta MHB=\Delta MKC\left(\text{câu a}\right)\)
\(\Rightarrow\widehat{BHM}=\widehat{CKM}\left(\text{2 góc tương ứng}\right)\left(4\right)\)
\(\text{Mà }\widehat{BHM}=90^o\left(5\right)\)
\(\text{Từ (4) và (5)}\Rightarrow\widehat{BHM}=\widehat{CKM}=90^o\left(6\right)\)
\(\text{Mà 2 góc này ở vị trí so le trong của 2 đường thẳng BH và CK}\left(7\right)\)
\(\text{Từ (6) và (7)}\Rightarrow BH\text{//}CK\left(\text{dấu hiệu nhận biết}\right)\)
\(\text{Hay }AH\text{//}CK\)
\(\Rightarrow\widehat{HAK}=\widehat{CKA}\left(\text{2 góc so le trong}\right)\)
\(\text{Ta có: }\widehat{AHM}+\widehat{IAH}=90^o+90^o=180^o\left(do\widehat{AHM}=\widehat{IAH}=90^o\right)\)
\(\text{Hay }\widehat{KHA}+\widehat{CAH}=180^o\left(8\right)\)
\(\text{2 góc này ở vị trí trong cùng phía của 2 đường thẳng CA và HK}\left(9\right)\)
\(\text{Từ (8) và (9)}\Rightarrow CA\text{//}HK\left(\text{dấu hiệu nhận biết}\right)\)
\(\Rightarrow\widehat{HKA}=\widehat{CAK}\left(\text{2 góc so le trong}\right)\)
\(\text{Xét }\Delta AHK\text{ và }\Delta KCAcó:\)
\(\widehat{HAK}=\widehat{CKA}\left(cmt\right)\left(10\right)\)
\(AK\text{ chung}\left(11\right)\)
\(\widehat{HKA}=\widehat{CAK}\left(cmt\right)\left(12\right)\)
\(\text{Từ (10), (11) và (12)}\Rightarrow\Delta AHK=\Delta KCA\left(g.c.g\right)\)
\(\Rightarrow HK=AC\left(\text{2 cạnh tương ứng}\right)\)
Chú ý: Do hoc24 không có cái dấu ngoặc cả 3 vào để suy ra 2 tam giác bằng nhau nên mình đánh dấu (1),(2),(3),... để suy ra nha, nếu bạn ghi vào vở thì chỉ cần ngoặc cả 3 cái vào rồi suy ra thôi
Để gõ hệ (hoặc các trường hợp dạng "hoặc"), ở dạng công thức trực quan em làm theo thứ tự khoanh đỏ:

Sau đó: 
Sau đó chọn loại hệ cần:

Nếu latex thì nhập vào hộp lệnh công thức:
\begin{cases} (các trường hợp cách nhau bằng \\) \end{cases}
Ví dụ: như em muốn để hệ 3 dạng tam giác bằng nhau thì nhập lệnh vào hộp TEX:
\begin{cases} \widehat{HAK}=\widehat{CKA}\\ AK \text{ chung} \\ \widehat{HKA}=\widehat{CAK} (\text{cmt}) \end{cases}
Nó sẽ hiển thị như sau:
\(\begin{cases} \widehat{HAK}=\widehat{CKA}\\ AK \text{ chung} \\ \widehat{HKA}=\widehat{CAK} (\text{cmt}) \end{cases}\)
Cần thêm các dòng lệnh nữa thì cứ thêm "\\ + lệnh" thôi

Vì AB=AC=> Tam giác ABC cân tại A
+) Tam giác ABC cân tại A có AM là tpg góc BAC
=> AM đồng thời là đường cao và đường trung tuyến
a) Do AM là đường trung tuyến
=> M là trung điểm BC
b) Do AM là đường cao
=> AM\(\perp\)BC
 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AM là cạnh chung
∠BAM = ∠CAM (cmt)
AB = AC (gt)
⇒ ∆ABM = ∆ACM (c-g-c)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
b) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
a) xét \(\Delta ABM\)và \(\Delta ACM\), có:
\(AB=AC\)(\(\Delta ABC\)cân tại A)
\(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
\(BM=CM\)(M là trung điểm của BC)
Do đó: \(\Delta ABM=\Delta ACM\)\(\left(c.g.c\right)\)
b) Vì \(\Delta ABM=\Delta ACM\)(câu a)
\(\Rightarrow\widehat{BMA}=\widehat{CMA}\)(2 góc tương ứng)
Mà \(\widehat{BMA}+\widehat{CMA}=180^0\)(kề bù)
\(\Rightarrow\widehat{BMA}=\widehat{CMA}=\frac{180^0}{2}=90^0\)
Xét \(\Delta ABM,\)vuông tại M (\(\widehat{BMA}=90^0\))
Theo định lí Py-ta-go, ta có:
\(AB^2=BM^2+AM^2\)
hay \(5^2=BM^2+\text{4^2}\)
\(\Rightarrow BM^2=25-16\)
\(BM^2=9\)
\(\Rightarrow BM=3\left(cm\right)\)
Vì M là trung điểm của BC (GT)
\(\Rightarrow BM=CM=\frac{BC}{2}\)
\(\Rightarrow2BM=BC\)
hay \(2\times5=BC\)
\(\Rightarrow BC=10\left(cm\right)\)
câu C mk ko bt làm
Mk cũng ko chắc đâu nha!!!
~Good luck~