Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có số đo cung \(AB=15+k2\pi,k\in\mathbb{Z}\)
\(15+k2\pi< 0\Leftrightarrow k< -\dfrac{15}{2\pi}\)
Vậy với \(k=-3\) ta được cung AB có số đo âm lớn nhất là \(15-6\pi\)
Chọn A.
Theo giả thiết ta có: 
suy ra điểm M là điểm chính giữa của cung phần tư thứ I.
Đáp án: C
Ta có:
Vậy cung (I) và (III) có điểm cuối trùng nhau
Chọn A.
Ta có: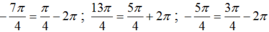 
Suy ra chỉ có hai cung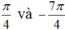 
có điểm cuối trùng nhau.
Chọn C.
Ta có 42000 = - 1200 + 12. 3600
nên cung có số đo – 1200 có ngọn cung trùng với ngọn cung có số đo 42000.
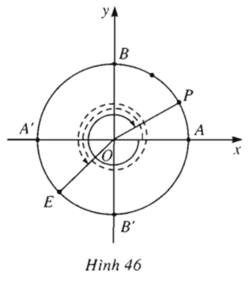
(OA, OE) = sđ cung(AE)= sđ cung(AB') + sđ cung(B'E) = - 90o + (-45)o = -135o = -3/4π (rad)
(OA, OP) = sđ cung(AP)= 1/3 sđ cung(AB) = 1/3 . 90° = 30o = π/6 rad.
Chọn C.
Nếu một góc lượng giác (Ou; Ov) có số đo α radian thì mọi góc lượng giác cùng tia đầu Ou, tia cuối Ov có số đo α + 2kπ, k ∈ Z, mỗi góc tương ứng với một giá trị của k.
Các cung lượng giác tương ứng trên đường tròn định hướng tâm O cũng có tính chất như vậy.
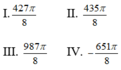
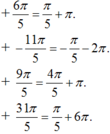
Ta có Sđ cung AB = 15 + k2π, k ∈ Z
15 + k2π < 0 ⇔ k < -15/2π
Vậy với k = -3 ta được cung AB có số đo âm lớn nhất là 15 - 6π