Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi q là công bội của cấp số. Khi đó ta có
u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11
⇔ u 2 + u 3 + u 4 = 39 11 u 1 + u 5 = 82 11 ⇔ u 1 q + q 2 + q 3 = 39 11 u 1 1 + q 4 = 82 11
Suy ra:
q 4 + 1 q 3 + q 2 + q = 82 39 ⇔ 39 q 4 − 82 q 3 − 82 q 2 − 82 q + 39 = 0
⇔ ( 3 q − 1 ) ( q − 3 ) ( 13 q 2 + 16 q + 13 ) = 0 ⇔ q = 1 3 , q = 3
q = 1 3 ⇒ u 1 = 81 11 ⇒ u n = 81 11 . 1 3 n − 1
q = 3 ⇒ u 1 = 1 11 ⇒ u n = 3 n − 1 11

Chọn C
Ta có S 2011 = u 1 q 2011 − 1 q − 1
q = 1 3 ⇒ S 2011 = 243 22 1 − 1 3 2011
q = 3 ⇒ S 2011 = 1 22 3 2011 − 1

Chọn C.
Công thức tổng quát của CSN có số hạng đầu là u1 và công bội q
u n = u 1 . q n - 1
Cách giải:
Gọi số hạng đầu và công bội của CSN lần lượt là u 1 , q
Theo đề bài ta có hệ phương trình:
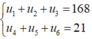
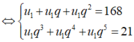
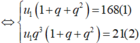
Lây (2) chia cho (1) ta được:
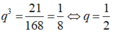
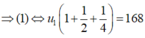
![]()

Để tìm U1 và q, ta sử dụng hệ phương trình sau:
U1 + U6 = 165U3 + U4 = 60Đầu tiên, ta sử dụng phương trình thứ hai để tìm U3: U3 = 60 - U4
Sau đó, thay giá trị của U3 vào phương trình thứ nhất: U1 + U6 = 165 U1 + (U3 + 3q) = 165 U1 + (60 - U4 + 3q) = 165 U1 - U4 + 3q = 105 (1)
Tiếp theo, ta sử dụng phương trình thứ nhất để tìm U6: U6 = 165 - U1
Thay giá trị của U6 vào phương trình thứ hai: U3 + U4 = 60 (60 - U4) + U4 = 60 60 = 60 (2)
Từ phương trình (2), ta thấy rằng phương trình không chứa U4, do đó không thể giải ra giá trị của U4. Vì vậy, không thể tìm được giá trị cụ thể của U1 và q chỉ từ hai phương trình đã cho.
Để tìm số hạng đầu và công bội của cấp số nhân, ta sử dụng các phương trình đã cho:
a. U4 - U2 = 72 U5 - U3 = 144
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U4: U4 = U2 + 72
Sau đó, thay giá trị của U4 vào phương trình thứ hai: U5 - U3 = 144 (U2 + 2q) - U3 = 144 U2 - U3 + 2q = 144 (3)
Từ phương trình (3), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
b. U1 - U3 + U5 = 65 U1 + U7 = 325
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U7: U7 = 325 - U1
Sau đó, thay giá trị của U7 vào phương trình thứ nhất: U1 - U3 + U5 = 65 U1 - U3 + (U1 + 6q) = 65 2U1 - U3 + 6q = 65 (4)
Từ phương trình (4), ta thấy rằng phương trình không chứa U3, do đó không thể giải ra giá trị của U1 và q chỉ từ hai phương trình đã cho.
c. U3 + U5 = 90 U2 - U6 = 240
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U6: U6 = U2 - 240
Sau đó, thay giá trị của U6 vào phương trình thứ nhất: U3 + U5 = 90 U3 + (U2 - 240 + 4q) = 90 U3 + U2 - 240 + 4q = 90 U3 + U2 + 4q = 330 (5)
Từ phương trình (5), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
d. U1 + U2 + U3 = 14 U1 * U2 * U3 = 64
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U3: U3 = 14 - U1 - U2
Sau đó, thay giá trị của U3 vào phương trình thứ hai: U1 * U2 * (14 - U1 - U2) = 64
Phương trình này có dạng bậc ba và không thể giải ra giá trị cụ thể của U1 và U2 chỉ từ hai phương trình đã cho.
Tóm lại, không thể tìm được giá trị cụ thể của số hạng đầu và công bội của cấp số nhân chỉ từ các phương trình đã cho.

Ta có
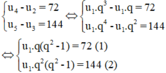
Lấy (2) chia (1) theo vế với vế ta được q = 2 thế vào (1):
(1) ⇔ 2u1(4 – 1) = 72 ⇔ u1 = 12
Vậy u1 = 12 và q = 2
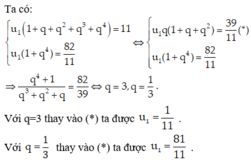
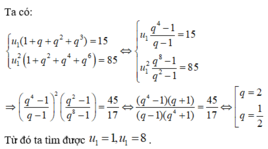
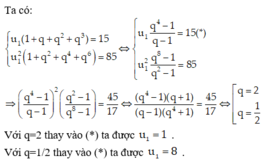
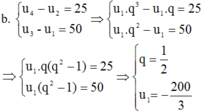
\(\left\{{}\begin{matrix}u1+u2+u3=13\\u4-u1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1\cdot q+u_1\cdot q^2=13\\u_1\cdot q^3-u_1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1+q+q^2}{\left(q-1\right)\left(q^2+q+1\right)}=\dfrac{13}{26}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{q-1}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}q-1=2\\u_1=\dfrac{26}{q^3-1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}q=2+1=3\\u_1=\dfrac{26}{3^3-1}=1\end{matrix}\right.\)
Tổng 8 số hạng đầu của cấp số nhân là:
\(\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1\cdot\left(1-3^8\right)}{1-3}=3280\)
\(\left\{{}\begin{matrix}u_1+u_2+u_3=13\\u_4-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1+u_1.q+u_1.q^2=13\\u_1.q^3-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q-1\right)\left(q^2+q+1\right)=26\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}13.\left(q-1\right)=26\\u_1.\left(q^3-1\right)=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}q=3\\u_1=1\end{matrix}\right.\)
\(S_8=\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1.\left(1-3^8\right)}{1-3}=3280\)