Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

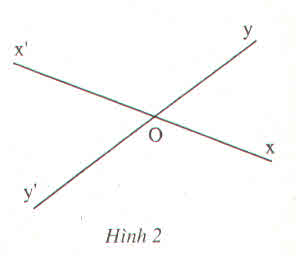
a) Góc xOy và góc .....là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
ghi ngắn gọn là ( ghi mỗi đáp án)
a) X'OY'
b) là hai góc đối đỉnh
+) Của cạnh OX' và cạnh OY là tia đối của cạnh OY'

A B C H D E
a) Xét \(\Delta\)ABH và \(\Delta\)ADH có :
BH = DH (gt)
góc AHB = góc AHD ( = 90 độ )
AH chung
=> \(\Delta\)ABH = \(\Delta\)ADH (c.g.c)
=> AB = AD ( hai cạnh tương ứng )
=> \(\Delta\)ABD cân tại A , mà góc ABD = 60 độ ( Do góc ABC = 60 độ )
=> \(\Delta\)ABD là tam giác đều (đpcm)
b) Do \(\Delta\)ABD đều
=> góc BAD = 60 độ
=> góc DAC = 30 độ (1)
Xét \(\Delta\)ABC có : góc A = 90 độ, góc B = 60 độ
=> góc C = 30 độ hay góc ACD = 30 độ (2)
Từ (1) và (2) => \(\Delta\)ADC cân tại D
=> AD = DC và góc ADC = 120 độ
=> góc HDE = 120 độ ( đối đỉnh với góc ADC )
Xét \(\Delta\)AHD và \(\Delta\)CED có :
góc AHD = góc CED ( = 90 độ )
AD = CD (cmt)
góc ADH = góc CDE ( đối đỉnh )
=> \(\Delta\)AHD = \(\Delta\)CED ( cạnh huyền - góc nhọn )
=> HD = ED ( hai cạnh tương ứng )
=> \(\Delta\)HDE cân tại E, có góc HDE = 120 độ (cmt)
=> góc DHE = góc DEH = 30 độ
Ta thấy : góc DHE = góc DCA = 30 độ , mà hai góc này ở vị trí sole trong
=> HE // AC (3)
Lại có : góc BAC = 90 độ \(\Rightarrow AB\perp AC\) (4)
Từ (3) và (4) => \(HE\perp AB\) (đpcm)

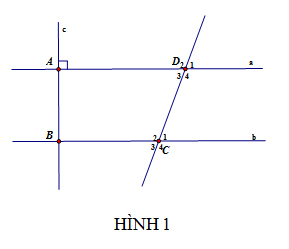
trc hết D1= 70O
a) D1 = D3= 70 (đối đỉnh)
C2 + D3 = 110+70 = 180 ( 2 góc này ở
vị trí trong cùng phía) nên a//b
b) theo a) có a//b
mà c vuông góc với a => c vuong goc voi b

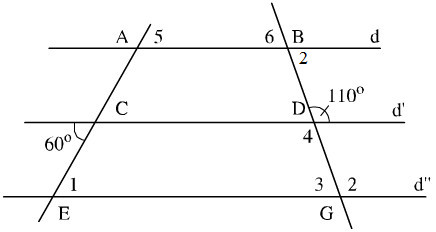
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì d’ //d’’ có: \(\widehat{E}_1\) và góc 600 là hai góc so le trong nên \(\widehat{E}_1\)= 600
+Vì d’ // d’’ có: \(\widehat{G}_2\)và góc 1100 là hai góc đồng vị nên \(\widehat{G_2}\) = 1100
+ \(\widehat{G}_2\)+\(\widehat{G}_3\)=\(180^0\) (hai góc kề bù)
Nên \(\widehat{G_3}=180^0-\widehat{G}_2=180^0-110^0=70^0\)
+) \(\widehat{D}_4\)1100 (vì là hai góc đối đỉnh)
+) \(\widehat{A}_5\) = \(\widehat{A}_1\) (Hai góc đối đỉnh)
Mà \(\widehat{A}_1\)= 600 (vì là hai góc đồng vị)
Nên \(\widehat{A}_5\) = 600 .
+ \(\widehat{B}_6\) = \(\widehat{B}_2\)(vì là hai góc đối đỉnh)
Mà \(\widehat{B}_2\) + 1100 = 1800 (hai góc trong cùng phía)
Nên \(\widehat{B}_2\) = 1800 - 1100 = 700.
Do đó: \(\widehat{B}_6\) = 700
a) Năm cặp đường thẳng vuông góc là:
d3 ⊥ d4; d3 ⊥ d5; d3 ⊥ d7; d1 ⊥ d8; d1 ⊥ d2
b) Bốn cặp đường thẳng song song là: d4//d5; d5//d7; d4//d7; d8//d2

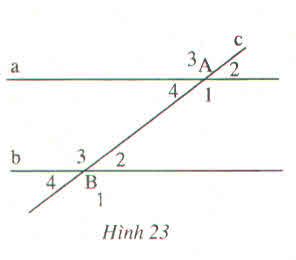
a) ˆB3B3^
b) ˆB2B2^
c) 1800 ; là cặp góc trong cùng phía
d) Bằng cặp góc so le trong ˆB2B2^=ˆA4A4^.
a) \(\widehat{A_1}\)\(=\widehat{B_3}\)(vì là cặp góc so le trong)
b)\(\widehat{A_2}\)\(=\widehat{B_2}\)(vì là cặp góc đồng vị)
c)\(\widehat{B_3}\)\(+\widehat{A_4}\)\(=180^0\)(vì là cặp góc trong cùng phía)
d)\(\widehat{A_2}\)\(=\widehat{B_4}\)(vì là cặp góc cùng bằng \(\widehat{A_4}\) )
Ủng hộ mk nhé!!! ^.^

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Rightarrow\) \(\begin{cases} a = bk \\ c = dk \end{cases}\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(1\right)\)
\(\dfrac{a.c}{b.d}=\dfrac{bk.dk}{b.d}=\dfrac{k^2.b.d}{b.d}=k^2\left(2\right)\)
Từ (1) và (2) suy ra: \(\dfrac{a.c}{b.d}=\dfrac{a^2+c^2}{b^2+d^2}\) \(\rightarrow đpcm\).
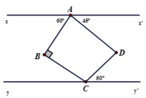

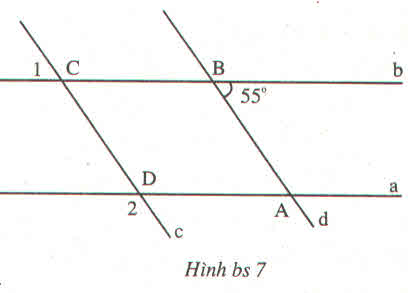

Vẽ các tia Bm và Dn lần lượt song song song với xx' như hình.
Suy ra Bm và Dn cũng song song với yy'
Khi đó: A B m ^ = x A B ^ = 60 o (so le trong)
⇒ m B C ^ = 30 o ⇒ B C y ^ = m B C ^ = 30 o .
Lại có: A D n ^ = D A x ' ^ = 45 o ; n D C ^ = D C y ' ^ = 50 o (so le trong).
Do đó: A D C ^ = 95 o .