Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
\(a=\lim\limits_{x\rightarrow-\infty}\frac{2\left|x\right|+1}{3x-1}=\lim\limits_{x\rightarrow-\infty}\frac{-2x+1}{3x-1}=\lim\limits_{x\rightarrow-\infty}\frac{-2+\frac{1}{x}}{3-\frac{1}{x}}=-\frac{2}{3}\)
\(b=\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{9+\frac{1}{x}+\frac{1}{x^2}}-\sqrt{4+\frac{2}{x}+\frac{1}{x^2}}}{1+\frac{1}{x}}=\frac{\sqrt{9}-\sqrt{4}}{1}=1\)
\(c=\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{1+\frac{2}{x}+\frac{3}{x^2}}+4+\frac{1}{x}}{\sqrt{4+\frac{1}{x^2}}+\frac{2}{x}-1}=\frac{1+4}{\sqrt{4}-1}=5\)
\(d=\lim\limits_{x\rightarrow+\infty}\frac{\frac{3}{x}-\frac{2}{x\sqrt{x}}+\sqrt{1-\frac{5}{x^3}}}{2+\frac{4}{x}-\frac{5}{x^2}}=\frac{1}{2}\)
Bài 2:
\(a=\lim\limits_{x\rightarrow-\infty}\frac{2+\frac{1}{x}}{1-\frac{1}{x}}=2\)
\(b=\lim\limits_{x\rightarrow-\infty}\frac{2+\frac{3}{x^3}}{1-\frac{2}{x}+\frac{1}{x^3}}=2\)
\(c=\lim\limits_{x\rightarrow+\infty}\frac{x^2\left(3+\frac{1}{x^2}\right)x\left(5+\frac{3}{x}\right)}{x^3\left(2-\frac{1}{x^3}\right)x\left(1+\frac{4}{x}\right)}=\frac{15}{+\infty}=0\)
a) 
(x4 – x2 + x - 1) = x4(1 - 
) = +∞.
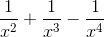b) 
(-2x3 + 3x2 -5 ) = x3(-2 +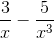 
) = +∞.
c) 
= 
= +∞.
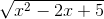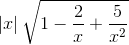d) \(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}+x}{5-2x}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left|x\right|\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{x\sqrt{1+\dfrac{1}{x^2}}+x}{5-2x}\)\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{1+\dfrac{1}{x^2}}+1}{\dfrac{5}{x}-2}=-1\).
Giới hạn của dãy nên bạn tự hiểu n tiến tới dương vô cực
1.
\(lim\frac{3n+1}{\sqrt[3]{\left(n^3+3n+1\right)^2}+n\sqrt{n^3+3n+1}+n^2}=lim\frac{3+\frac{1}{n}}{\sqrt[3]{\frac{\left(n^3+3n+1\right)^2}{n^3}}+\sqrt{n^3+3n+1}+n}=\frac{3}{\infty}=0\)
b=\(lim\left(\sqrt[3]{n^3+2n}-n+n-\sqrt{n^2+1}\right)=lim\left(\frac{2n}{\sqrt[3]{\left(n^3+2n\right)^2}+n\sqrt[3]{n^3+2n}+n^2}-\frac{1}{n+\sqrt{n^2+1}}\right)\)
\(=lim\left(\frac{2}{\sqrt[3]{\frac{\left(n^3+2n\right)^2}{n^3}}+\sqrt[3]{n^3+2n}+n}-\frac{1}{n+\sqrt{n^2+1}}\right)=0-0=0\)
c\(=lim\left(\frac{2n^2+n}{\sqrt[3]{\left(n^3+n\right)^2}+\sqrt[3]{\left(n^3+n\right)\left(n^3-2n^2\right)}+\sqrt[3]{\left(n^3-2n^2\right)^2}}\right)\)
\(=lim\left(\frac{2+\frac{1}{n}}{\sqrt[3]{\left(1+\frac{1}{n^2}\right)^2}+\sqrt[3]{\left(1+\frac{1}{n^2}\right)\left(1-\frac{2}{n}\right)}+\sqrt[3]{\left(1-\frac{2}{n}\right)^2}}\right)=\frac{2}{1+1.1+1}=\frac{2}{3}\)
2.
a\(=lim\left[n\left(2-\sqrt{1+\frac{3}{n}}\right)\right]=+\infty\left(2-1\right)=+\infty\)
\(b=lim\left[n\left(\sqrt{1+\frac{2}{n^2}}-\sqrt{\frac{3}{n}+\frac{1}{n^2}}\right)\right]=+\infty\left(1-0\right)=+\infty\)
\(c=lim\left[n^3\left(\frac{sin2n}{n^2}-3\right)\right]=+\infty\left(0-3\right)=-\infty\)
\(\lim\limits_{x\rightarrow-\infty}\frac{ax^2-4x+5}{2x^2+x+1}=\lim\limits_{x\rightarrow-\infty}\frac{a-\frac{4}{x}+\frac{5}{x^2}}{2+\frac{1}{x}+\frac{1}{x^2}}=\frac{a}{2}=4\)
\(\Rightarrow a=8\)
\(\Rightarrow\) Có đúng 1 số thực a thỏa mãn
16.
\(y'=\frac{\left(cos2x\right)'}{2\sqrt{cos2x}}=\frac{-2sin2x}{2\sqrt{cos2x}}=-\frac{sin2x}{\sqrt{cos2x}}\)
17.
\(y'=4x^3-\frac{1}{x^2}-\frac{1}{2\sqrt{x}}\)
18.
\(y'=3x^2-2x\)
\(y'\left(-2\right)=16;y\left(-2\right)=-12\)
Pttt: \(y=16\left(x+2\right)-12\Leftrightarrow y=16x+20\)
19.
\(y'=-\frac{1}{x^2}=-x^{-2}\)
\(y''=2x^{-3}=\frac{2}{x^3}\)
20.
\(\left(cotx\right)'=-\frac{1}{sin^2x}\)
21.
\(y'=1+\frac{4}{x^2}=\frac{x^2+4}{x^2}\)
22.
\(lim\left(3^n\right)=+\infty\)
11.
\(\lim\limits_{x\rightarrow1^+}\frac{-2x+1}{x-1}=\frac{-1}{0}=-\infty\)
12.
\(y=cotx\Rightarrow y'=-\frac{1}{sin^2x}\)
13.
\(y'=2020\left(x^3-2x^2\right)^{2019}.\left(x^3-2x^2\right)'=2020\left(x^3-2x^2\right)^{2019}\left(3x^2-4x\right)\)
14.
\(y'=\frac{\left(4x^2+3x+1\right)'}{2\sqrt{4x^2+3x+1}}=\frac{8x+3}{2\sqrt{4x^2+3x+1}}\)
15.
\(y'=4\left(x-5\right)^3\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{ax^2+bx}-cx\right)=\lim\limits_{x\rightarrow+\infty}\frac{\left(a-c^2\right)x^2+bx}{\sqrt{ax^2+bx}+cx}=\lim\limits_{x\rightarrow+\infty}\frac{\left(a-c^2\right)x+b}{\sqrt{a+\frac{b}{x}}+c}\)
Để giới hạn đã cho là hữu hạn bằng -2
\(\Leftrightarrow\left\{{}\begin{matrix}c^2+a=18\\a-c^2=0\\\frac{b}{\sqrt{a}+c}=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=9\\c^2=9\\\frac{b}{3+c}=-2\end{matrix}\right.\) \(\left(c\ne-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a=9\\c=3\\c=-12\end{matrix}\right.\) \(\Rightarrow P=12\)