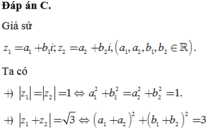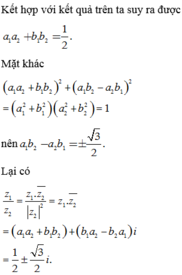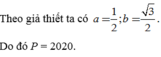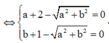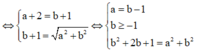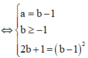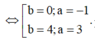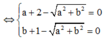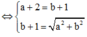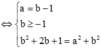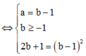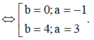Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Gọi M(x;y) là điểm biều diễn số phức z.
Từ giả thiết, ta có |z - 4 - 3i| =
5
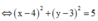
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB với A(-1;3), B(1;-1)
Ta có 
Gọi E(0;1) là trung điểm của AB 
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C)
Vậy 
Dấu “=”xảy ra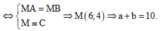 
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có 
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có
Gọi E(0;1) là trung điểm của AB
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy 
Dấu “=” xảy ra 
=> a + b = 10
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có 
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R =
5
. Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có: 
Gọi E(0;1) là trung điểm của AB 
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy 
Dấu “=” xảy ra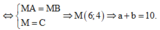 
\(z=x+yi\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2=x^2+y^2\)
\(\Rightarrow x+y+1=0\Rightarrow\) tập hợp z là đường thẳng d: \(x+y+1=0\)
\(P=\left|\left(z-4-5i\right)-\left(w-3-4i\right)\right|\ge\left|\left|z-4-5i\right|-\left|w-3-4i\right|\right|=\left|\left|z-4-5i\right|-1\right|\)
Gọi M là điểm biểu diễn z và \(A\left(4;5\right)\Rightarrow\left|z-4-5i\right|=AM\)
\(AM_{min}=d\left(A;d\right)=\dfrac{\left|4+5+1\right|}{\sqrt{1^2+1^2}}=5\sqrt{2}\)
\(\Rightarrow P\ge\left|5\sqrt{2}-1\right|=5\sqrt{2}-1\)
Đáp án A.
Phương pháp:
Từ 
tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
nhỏ nhất
Cách giải: Gọi z=x+ui ta có:
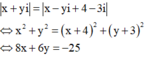
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
nhỏ nhất.
Ta có: 
Dấu bằng xảy ra 
M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có 
Phương trình đường trung trực của AB là
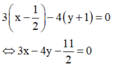
Để 
Tọa độ điểm M là nghiệm của hệ phương trình
Đáp án D
Cách 1
· Đặt 
biểu diễn cho số phức z.
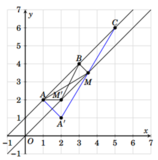
· Từ giả thiết, ta có M thuộc đường trung trực 
của đoạn EF và P=AM+BM+CM
· Ta chứng minh điểm M chính là hình chiếu vuông góc của B lên đường thẳng ∆ .
- Với M’ tùy ý thuộc ∆ , M’ khác M. Gọi A’ là điểm đối xứng của A qua ∆ . Nhận thấy rằng ba điểm A’, M, C thẳng hàng.
- Ta có 
Mà 
Lại có 
Do đó 
Cách 2
· Gọi 
Từ giả thiết 
, dẫn đến y=x .
Khi đó z=x+xi.
· 
· Sử dụng bất đẳng thức 
Dấu đẳng thức xảy ra khi và chỉ khi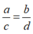 
. Ta có
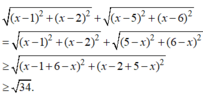
Dấu đẳng thức xảy ra khi và chỉ khi 
· Mặt khác
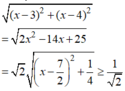
Dấu đẳng thức xảy ra khi và chỉ khi x= 7 2
· Từ hai trường hợp trên, ta thấy, giá trị nhỏ nhất của P là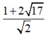 
.
Khi đó a+b=3.
Đáp án D.
Đặt z = a + bi => a + bi 
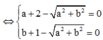
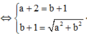
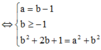
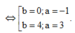
Do |z| > 1 => a = 3, b = 4
