Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5. ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\) \(a.b=c.d\)
\(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2-2ab}{\left(c+d\right)^2-2cd}\)
Mà a+b = c+ d; ab = cd
=> đfcm
Bài 4:
a: Ta có: I nằm trên đường trung trực của AD
nên IA=ID
Ta có: I nằm trên đường trung trực của BC
nên IB=IC
b: Xét ΔIAB và ΔIDC có
IA=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔIAB=ΔIDC

Xét ΔAID=ΔBIC có:
IA=IB(gt)
IC=ID(gt)
góc AID=góc CIB
Vậy ΔAID=ΔBIC (c-g-c)
=>góc IBC=góc DAB (2 góc tương ứng)
Mà góc IBC và góc DAB là hai góc so le trong
=>AD//BC (dấu hiệu nhận biết)
Vì ΔAID=ΔBIC
=>AD=CB (2 cạnh tương ứng)
Mà M,N lần lượt là trung điểm của AD và BC=>AM=NB
Xét t/g AIM và t/g BIN có :
AI=IB(gt)
NB=AM(cmt)
góc MAI=góc IBN (cmt)
Vậy t/g AIM=t/g BIN (c-g-c)
=>MI=NI (2 cạnh tương ứng)
Vì t/g AIM=t/g BIN =>góc AIM=góc NIB (2 góc tương ứng)
Mà góc AIM+góc AIN=180 độ
=>góc NIB+góc AIN=180 độ
=>M,I,N thẳng hàng

a ) Xét Δ AHB và Δ AHC có :
AB = AC ( GT )
Góc AHB = góc AHC
AH là cạnh chung
=> tam giác AHB = tam giác AHC ( cạnh huyền - cạnh góc vuông )

BẠn tự vẽ hình nha:
MÌnh không chắc cách làm này phù hợp không,đây là cách chậm và dễ hiểu nhất:
a)Vì ACI+AIC+CAI=1800( tổng 3 góc cua 1 tam giác)
=> ACI+CAI=900 (1)
Vì CIB+IBC+BCI=180(như trên)
=>IBC+BCI=900 (2)
Mà IBC=CAI (tam giac ACB cân- có CA=CB=10 Cm)
=> tu 1 và 2 =>ACI=BCI
Xét tam giác CAI và CBI, có:
ACI=BCI( ở trên)
CAI=CBI (tam giác ABC cân)
CA=CB=10 cm
=> tam giác CAI= tg CBI
=>AI=BI ( 2 cạnh tương ứng)
b) Xét tg CHI và CKI, có:
HCI=KCI (vì có BCI=ACI-câu a)
CI cạnh chung
=> tg CHI= tg CKI ( cạnh huyền-góc nhọn)
=> HI= KI
c) IA=IB(câu a) => IA = AB :2=12:2=6 (cm)
Áp dụng định lí Py-ta-go trong tg CBI,có:
IC2=CB2-IB2
=> IC=8(cm) (bạn tự lắp số vào nha)
d) vì tg CHI=tg CKI (cm ở b)
=> CH=CK => tg CHK cân ở C => CHK=CKH=(1800-HCK):2 (1)
tg CAB cân=> CAB=CBA=(1800-ACB):2=(1800-HCK):2 (2)
từ 1)và (2)=>CHK=CAB
MÀ chúng là 2 góc đồng vị
=>HK song song AB

- ΔAOD = ΔCOB
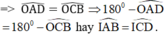
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
- Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
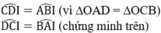
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
Đặt\(A=\left|a-b\right|+\left|b-c\right|+\left|c-d\right|+\left|d-a\right|\)
\(\Rightarrow A=\left|a-b\right|+\left(a-b\right)+\left|b-c\right|+\left(b-c\right)\)
\(+\left|c-d\right|+\left(c-d\right)+\left|d-a\right|+\left(d-a\right)\)
Ta có: \(\left|x\right|+x=\hept{\begin{cases}2x,x\ge0\\0,x\le0\end{cases}}\)nên \(\left|x\right|+x\)luôn là số chẵn.
Vậy A là số chẵn hay \(\left|a-b\right|+\left|b-c\right|+\left|c-d\right|+\left|d-a\right|\)luôn chẵn