Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vì đt $y=ax+b$ song song với $y=2x+2019$ nên $a=2$
$y=ax+b$ cắt trục tung tại điểm có tung độ $2020$, nghĩa là $(0,2020)\in (y=ax+b)$
$\Leftrightarrow 2020=a.0+b$
$\Rightarrow b=2020$
Vậy $a=2; b=2020$

a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
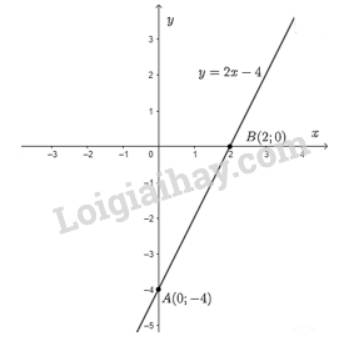
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

a: 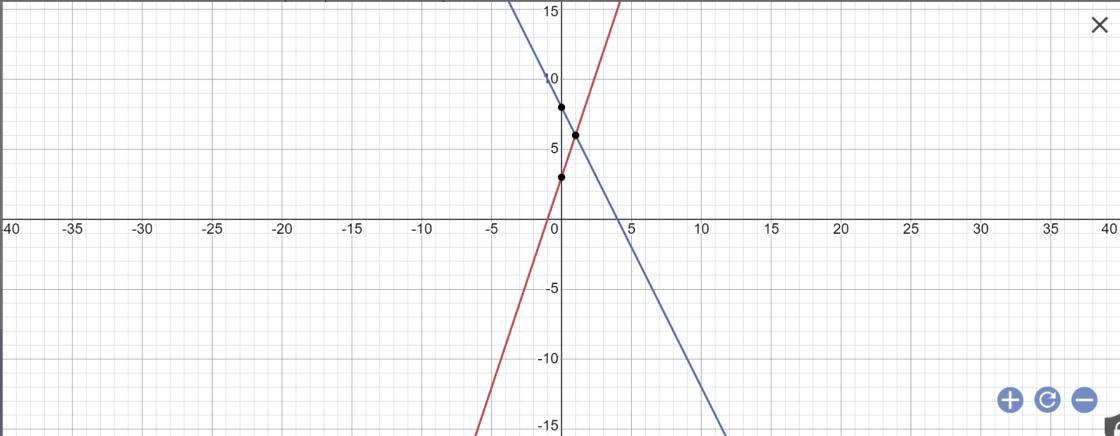
b: Tọa độ A là:
\(\left\{{}\begin{matrix}3x+3=-2x+8\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-2+8=6\end{matrix}\right.\)
Vậy: A(1;6)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\3x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-2x+8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-2x=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
Vậy: A(1;6); B(-1;0); C(4;0)
\(AB=\sqrt{\left(-1-1\right)^2+\left(0-6\right)^2}=2\sqrt{10}\)
\(AC=\sqrt{\left(4-1\right)^2+\left(0-6\right)^2}=3\sqrt{5}\)
\(BC=\sqrt{\left(4+1\right)^2+\left(0-0\right)^2}=5\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot BA\cdot AC}=\dfrac{40+45-25}{2\cdot2\sqrt{10}\cdot3\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot2\sqrt{10}\cdot3\sqrt{5}=15\)
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
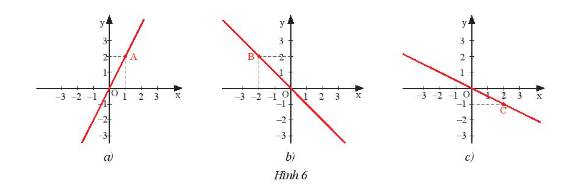
b) Các đồ thị sau đây là đồ thị của hàm số nào?

a)
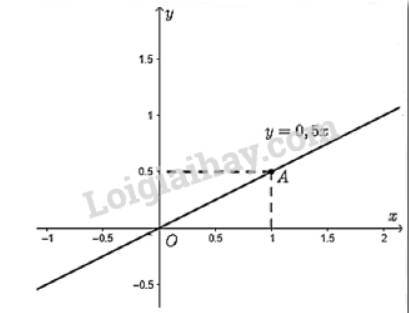
- Vẽ đồ thị hàm số \(y = 0,5x\)
Cho \(x = 1 \Rightarrow y = 0,5.1 = 0,5\). Ta vẽ điểm \(A\left( {1;0,5} \right)\)
Đồ thị hàm số \(y = 0,5x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;0,5} \right)\).
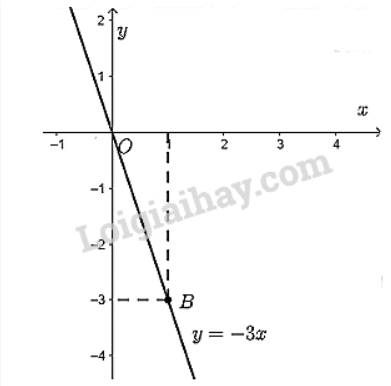
- Vẽ đồ thị hàm số \(y = - 3x\)
Cho \(x = 1 \Rightarrow y = - 3.1 = - 3\). Ta vẽ điểm \(B\left( {1; - 3} \right)\)
Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(B\left( {1; - 3} \right)\).
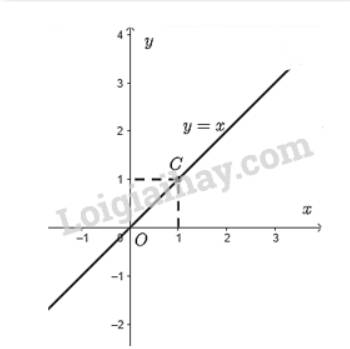
- Vẽ đồ thị hàm số \(y = x\)
Cho \(x = 1 \Rightarrow y = 1\). Ta vẽ điểm \(C\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(C\left( {1;1} \right)\).
b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ \(O\left( {0;0} \right)\) nên có dạng \(y = ax\).
- Ở đồ thị a, đồ thị hàm số đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a.1 \Rightarrow a = 2\).
Do đó, đồ thị a là đồ thị của hàm số \(y = 2x\).
- Ở đồ thị b, đồ thị hàm số đi qua điểm \(B\left( { - 2;2} \right)\) nên ta có: \(2 = a.\left( { - 2} \right) \Rightarrow a = 2:\left( { - 2} \right) = - 1\).
Do đó, đồ thị b là đồ thị của hàm số \(y = - x\).
- Ở đồ thị c, đồ thị hàm số đi qua điểm \(C\left( {2; - 1} \right)\) nên ta có: \( - 1 = a.2 \Rightarrow a = \left( { - 1} \right):2 = \dfrac{{ - 1}}{2}\).
Do đó, đồ thị b là đồ thị của hàm số \(y = \dfrac{{ - 1}}{2}x\).

a: Thay x=-1 và y=-2 vào y=(m-1)x+2m, ta được:
\(-\left(m-1\right)+2m=-2\)
=>2m-m+1=-2
=>m+1=-2
=>m=-3
b: Khi m=-1 thì \(y=\left(-1-1\right)x+2\cdot\left(-1\right)=-2x-2\)
Lời giải:
a.
Vẽ đồ thị hàm số $y=2x-2$
Cho $x=0$ thì $y=2.0-2=-2$. Ta có điểm $A(0;-2)$
Cho $x=1$ thì $y=2.1-2=0$. Ta có điểm $B(1;0)$
Nối 2 điểm $A,B$ ta có đồ thị hàm số $y=2x-2$
Thực hiện tương tự với 2 ĐTHS còn lại
b.
Hệ số góc của $y=2x-2$ là $2$
Hệ số góc của $y=-x+2$ là $-1$
Hệ số góc của $y=2x+1$ là $2$
cho hình cụ thể được kh ạ