Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Thay m = -1/2 vào (d) ta được :
\(y=2x-2.\left(-\frac{1}{2}\right)+2\Rightarrow y=2x+3\)
Hoành độ giao điểm thỏa mãn phương trình
\(2x+3=x^2\Leftrightarrow x^2-2x-3=0\)
\(\Delta=4-4\left(-3\right)=4+12=16>0\)
\(x_1=\frac{2-4}{2}=-1;x_2=\frac{2+4}{2}=3\)
Vói x = -1 thì \(y=-2+3=1\)
Vớ x = 3 thì \(y=6+3=9\)
Vậy tọa độ giao điểm của 2 điểm là A ( -1 ; 1 ) ; B ( 3 ; 9 )
b, mình chưa học
\(y_1+y_2=4\left(x_1+x_2\right)\)
\(\Leftrightarrow x_1^2+x_2^2=4\left(x_1+x_2\right)\)(1)
Xét phương trình hoành độ giao điểm của (d) và (P) ta có:
\(x^2=2x-2m+2\)
\(\Leftrightarrow x^2-2x+2m-2=0\)
Theo hệ thức Vi-et ta có:
\(\hept{\begin{cases}x_1+x_2=2\\x_1x_2=2m-2\end{cases}}\)
Từ (1) \(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\left(x_1+x_2\right)\)
\(\Leftrightarrow4-4m+4=8\)
\(\Leftrightarrow m=0\)
vậy..

để (d) song song zới đường thẳng (d')
=>\(\hept{\begin{cases}m+1=3\\-2m\ne4\end{cases}=>\hept{\begin{cases}m=2\\m\ne-2\end{cases}=>m=2}}\)
b)phương trình hoành độ giao điểm của (d) zà (P)
\(\frac{1}{2}x^2-\left(m+1\right)x+2m=0\Rightarrow x^2-2\left(m+1\right)x+4m=0\)
ta có \(\Delta=4\left(m+1\right)^2-4.4m=4\left(m^2+2m+1\right)-16m=4m^2-8m+4=4\left(m-1\right)^2\ge0\)
để d cắt P tại hai điểm phân biệt
=>\(\Delta>0=>\left(m-1\right)^2>0=>m\ne1\)(1)
lại có \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=4m\end{cases}}\)
để 2 hoành độ dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2>0\\x_1x_2>0\end{cases}=>\hept{\begin{cases}2\left(m+1\right)>0\\4m>0\end{cases}=>\hept{\begin{cases}m>-1\\m>0\end{cases}\Rightarrow m>0}}\left(2\right)}\)
từ 1 zà 2 => m khác 1 , m lớn hơn 0 thì (d) cắt (P) tạ điểm phân biệt có hoành độ dương

Mình nghĩ nên sửa đề y=2(m-1)x-m2+6 và parobol (P)y=x2
a) Với m=3 ta được (d): y=4x-3
Hoành độ giao điểm của đường thẳng (d) và parabol (P0 là nghiệm của phương trình \(x^2=4x-3\)
<=> x2-4x+3=0
<=> x2-3x-x+3=0
<=> x(x-3)-(x-3)=0
<=> (x-3)(x-1)=0
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\Rightarrow y=1\\x=3\Rightarrow y=9\end{cases}}}\)
Vậy giao điểm của (d) và (P) là A(1;1); B(3;9)
b) Phương trình hoành độ của (d) cắt (P) là nghiệm của phương trình x2-2(m-1)x-m2+6
<=> x2-2(m-1)x+m2-6=0 (1)
<=> (m-1)2-(m2-6)=7-2m
Đường thẳng (d) cắt (P) tại 2 điểm phân biệt khi và chỉ khi phương trình (1) có 1 nghiệm phân biệt
<=> 7-2m>0
<=> \(m< \frac{7}{2}\)(*)
Gọi x1;x2 là nghiệm của phương trình (1)
Khi đó thoe định lý Vi-et ta có:
\(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1\cdot x_2+m^2=6\end{cases}}\)
Theo bài ra ta có: \(x_1^2+x_2^2=6\Leftrightarrow x_1+x_2^2+2x_1x_2=16\)
\(4\left(m^2-1\right)-2\left(m^2-6\right)=16\)
<=>2m2-8m=0
<=> m=0 hoặc m=4
m=0 (tmđk (*))
m=4 (ktmđk (*))
Vậy m=0 là giá trị cần tìm

Hãy tích cho tui đi
vì câu này dễ mặc dù tui ko biết làm
Yên tâm khi bạn tích cho tui
Tui sẽ ko tích lại bạn đâu
THANKS
a: Thay x=10 vào (d1), ta được:
\(y=2\cdot10-1=20-1=19\)
=>A(10;19) thuộc (d1)
Thay x=-4 vào (d1), ta được:
\(y=2\left(-4\right)-1=-8-1=-9\)
=>B(-4;-7) không thuộc (d1)
Thay x=-11 vào (d1), ta được:
\(y=2\cdot\left(-11\right)-1=-22-1=-23\)
=>C(-11;-23) thuộc (d1)
b: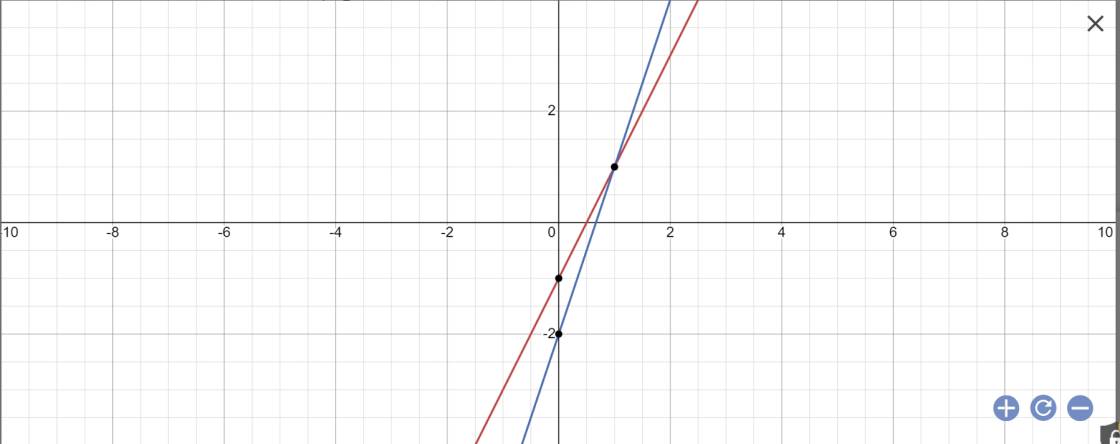
c: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=2x-1\\y=2x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2x=-1+2=1\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\cdot1-1=1\end{matrix}\right.\)
d: Để (d3) đồng quy với (d1),(d2) thì (d3) đi qua giao điểm của (d1) và (d2)
=>(d3) đi qua F(1;1)
Thay x=1 và y=1 vào (d3), ta được:
1(m-1)+3=1
=>m-1+3=1
=>m+2=1
=>m=-1