Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

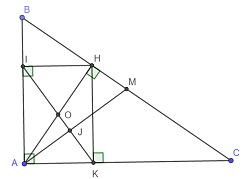
a) Xét tứ giác AIHK có \(\widehat{AIH}+\widehat{IAK}+\widehat{AKH}=270^o\Rightarrow\widehat{IHK}=90^o\)
Vậy nên \(HI\perp HK\)
b) Do IA và HK cùng vuông góc với AC nên IA // HK
Vậy thì \(\widehat{IAH}=\widehat{KHA}\) (So le trong)
Xét tam giác IAH và tam giác KHA có:
\(\widehat{AIH}=\widehat{HKA}=90^o\)
Cạnh AH chung
\(\widehat{IAH}=\widehat{KHA}\)
\(\Rightarrow\Delta AIH=\Delta HKA\) (Cạnh huyền - góc nhọn)
\(\Rightarrow IA=HK.\)
c) Xét tam giác IAH và tam giác HKI có:
\(\widehat{AIH}=\widehat{KHI}=90^o\)
Cạnh IH chung
\(IA=HK\)
\(\Rightarrow\Delta AIH=\Delta KHI\) (Hai cạnh góc vuông)
\(\Rightarrow AH=IK.\)
d) Ta thấy ngay các cặp góc so le trong bằng nhau nên \(\Delta IOA=\Delta KOH\left(g-c-g\right)\Rightarrow OI=OK,OA=OH\)
Xét tam giác vuông IAH có IO là trung tuyến ứng với cạnh huyền nên OH = OA = OI.
Vậy nên OA = OI = OH = OK.
e)
1. Nếu tam giác ABC cân thì AH là đường cao đồng thời trung tuyến. Vậy thì AH = BH = CH.
Xét tam giác cân BHA có HI là đường cao nên đồng thời là đường trung tuyến. Vậy nên I là trung điểm AB.
Hoàn toàn tương tự ta có K là trung điểm AC.
2. Tam giác ABC vuông cân tại A nên \(\widehat{ACB}=45^o\)
IA = AB/2; AK = AC/2 mà AB = AC nên AI = AK.
Vậy thì tam giác IAK cũng vuông cân tại A.
Vậy nên \(\widehat{AKI}=45^o\)
Từ đó ta có \(\widehat{AKI}=\widehat{ACB}=45^o\)
Chúng lại ở vị trí đồng vị nên suy ra IK // BC.
f) Ta có AM = MC nên \(\widehat{MAC}=\widehat{MCA}\)
Lại có \(\widehat{MCA}=\widehat{AHK}\) (Cùng phụ với góc \(\widehat{KHC}\) )
Suy ra \(\widehat{MAC}=\widehat{AHK}\)
Lại có \(\widehat{OKA}=\widehat{OHA}\)
Vậy nên \(\widehat{MAK}+\widehat{OKA}=\widehat{AHK}+\widehat{IHA}=90^o\)
Gọi J là giao điểm của AM và IK thì \(\widehat{AJK}=90^o\) hay \(KI\perp AM\)

a, xet tam giac ABD va tam giac ACD co : AD chung
AB = AC do tam giac ABC can tai A (gt)
goc BAD = goc CAD do AD la phan giac cua goc A (gt)
=> tam giac ABD = tam giac ACD (c - g - c)
=> BD = CD (dn)
xet tam giac BED va tam giac CFD co : goc BED = goc CFD = 90 do ...
goc B = goc C do tam giac ABC can tai A(gt)
=> tam giac BED = tam giac CFD (ch - gn)
=> DE = DF (dn)
b, cm o cau a
c, tam giac ABD = tam giac ACD (cau a)
=> goc ADC = goc ADB (dn)
goc ADC + goc ADB = 180 (kb)
=> goc ADC = 90
co DB = DC (cau a)
=> AD la trung truc cua BC (dn)

MA=MB; NB=NC => MN là đường trung bình của tg ABC => MN//AC (1)
Xét tg ACD và tg END có
^ADC = ^EDN (góc đối đỉnh)
CN=BC/2; CD=BC/4 => CD=CN/2 hay DC=DN
DA=DE
=> tg ACD = tg END (c.g.c) => ^DAC = ^DEN => EN//AC (2)
Từ (1) và (2) => MN trùng EN (Từ 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 dt // với đường thẳng đã cho)
=> M;N;E thẳng hàng
CẬU ƠI LỚP 7 ĐÃ HỌC ĐƯỜNG TRUNG BÌNH đâu , bài này tớ có cách khác
A B C D E M N
A) NỐI B VÀ E
TA CÓ
\(DC=\frac{1}{4}BC\left(1\right)\)
MÀ \(NC=\frac{1}{2}BC\)
THAY \(ND+DC=\frac{1}{2}BC\)
THAY (1) VÀO TA CÓ
\(ND+\frac{1}{4}BC=\frac{1}{2}BC\)
\(\Leftrightarrow ND=\frac{1}{2}BC-\frac{1}{4}BC\)
\(\Leftrightarrow ND=BC\left(\frac{1}{2}-\frac{1}{4}\right)\)
\(\Leftrightarrow ND=\frac{1}{4}BC\)
MÀ \(DC=\frac{1}{4}BC\)
\(\Rightarrow ND=DC\left(2\right)\)
TA LẠI CÓ \(BN=NC\left(gt\right)\)
THAY \(BN=ND+DC\)
THAY (2) VÀO TA CÓ
\(BN=2ND\)
MÀ \(BN+ND=BD\)
THAY \(2ND+ND=BD\)
\(\Leftrightarrow3ND=BD\)
\(\Leftrightarrow ND=\frac{1}{3}BD\)
VÌ AD = DE => BD LÀ ĐƯỜNG TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABE\)
MÀ \(ND=\frac{1}{3}BD\)
=> N LÀ TRỌNG TÂM CỦA \(\Delta ABE\)
VÌ AM=BM
=> EM LÀ ĐƯỜNG TRUNG TUYẾN THỨ 2 CỦA \(\Delta ABE\)
MÀ N LÀ TRỌNG TÂM CỦA \(\Delta ABE\)
=> EM BẮT BUỘT ĐI QUA N
=> BA ĐIỂM E,M,N THẲNG HÀNG (ĐPCM)

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
6a1 is real
Trên diễn đàn có thể có rất nhiều bạn tham gia giải toán. Vậy câu trả lời nào là đúng và tin cậy được? Các bạn có thể nhận biết các câu trả lời đúng thông qua 6 cách sau đây:
1. Lời giải rõ ràng, hợp lý (vì nghĩ ra lời giải có thể khó nhưng rất dễ để nhận biết một lời giải có là hợp lý hay không. Chúng ta sẽ học được nhiều bài học từ các lời giải hay và hợp lý, kể cả các lời giải đó không đúng.)
2. Lời giải từ các giáo viên của Online Math có thể tin cậy được (chú ý: dấu hiệu để nhận biết Giáo viên của Online Math là các thành viên có gắn chứ "Quản lý" ở ngay sau tên thành viên.)
3. Lời giải có số bạn chọn "Đúng" càng nhiều thì càng tin cậy.
4. Người trả lời có điểm hỏi đáp càng cao thì độ tin cậy của lời giải sẽ càng cao.
5. Các bài có dòng chữ "Câu trả lời này đã được Online Math chọn" là các lời giải tin cậy được (vì đã được duyệt bởi các giáo viên của Online Math.)
6. Các lời giải do chính người đặt câu hỏi chọn cũng là các câu trả lời có thể tin cậy được.