Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có: f(x) + h(x) = g(x)
Suy ra: h(x) = g(x) – f(x) = (x4 – x3 + x2 + 5) – (x4 – 3x2 + x – 1)
= x4 – x3 + x2 + 5 – x4 + 3x2 – x + 1
= -x3 + 4x2 – x + 6
b. Ta có: f(x) – h(x) = g(x)
Suy ra: h(x) = f(x) – g(x) = (x4 – 3x2 + x – 1) – (x4 – x3 + x2 + 5)
= x4 – 3x2 + x – 1 – x4 + x3 – x2 – 5
= x3 – 4x2 + x – 6

1.
a, (x-5)2
Ta có x2 luôn \(\ge\) 0 với mọi x, suy ra: (x-5)2 \(\ge\) 0 với mọi x
Nên: (x-5)2 \(\ge\) 0 với mọi x
Suy ra: đa thức này không có nghiệm.

a,f(x)+g(x)=\(\left(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\right)+\left(b_nx^{n-1}+...+b_1x+b_0\right)\)
=\(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0+b_nx^n+b_{n-1}x^{n-1+...+b_1x+b_0}\)
\(=\left(a_nx^n+b_nx^n\right)+\left(a_{n-1}x^{n-1}+b_{n-1}x^{n-1}\right)+...+\left(a_1x+b_1x\right)+\left(a_0+b_0\right)\)
b
f(x)+g(x)=\(\left(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\right)+\left(b_nx^n+b_{n-1}x^{n-1}+...+b_1x+b_0\right)\)
\(=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0-b_nx^n-b_{n-1}-b_1x+b_0\)
\(=(a_nx^n-b_nx^n)+(a_{n-1}x^{n-1}-b_{n-1}x^{n-1})+...+(a_1x-b_1x)+\left(a_0+b_0\right)\)
\(=\left(a_n-b_n\right)x^n+(a_{n-1}-b_{n-1})x^{n-1}+...+\left(a_1-b_1\right)x+\left(a_0-b_0\right)\)

a: \(=\dfrac{80}{9}x^3+\dfrac{1}{3}x^2-\dfrac{1}{3}x+18\)
Hệ số cao nhất là 80/9
Hệ số tự do là 18
Bậc là 3
b: \(f\left(3\right)=\dfrac{80}{9}\cdot27+\dfrac{1}{3}\cdot9-\dfrac{1}{3}\cdot3+18=260\)
\(f\left(-3\right)=\dfrac{80}{9}\cdot\left(-27\right)+\dfrac{1}{3}\cdot9+\dfrac{1}{3}\cdot3+18=-218\)
c: f(x)=-28 nên \(\dfrac{80}{9}x^3+\dfrac{1}{3}x^2-\dfrac{1}{3}x+46=0\)
\(\Leftrightarrow x\simeq-1.75\)

Bài 1:
a/ Kết quả: f(x) - g(x) + h(x) = 2x - 1
(tự ghép cặp vào r` tính hoặc tính = hàng dọc nhé bn, muộn r` , mk k muốn đánh máy)
b/ 2x - 1 = 0
<=> 2x = 1
<=> x = \(\dfrac{1}{2}\)
Vậy x = .... để f(x) - g(x) + h(x) = 0
Bài 2:
a/ dễ --> tự lm cko quen để đỡ mất căn bản nhé bn!
b/ sửa: g(x) = ..... + 2x3 + 3x
Làm: kết quả: 3x2 + 7x (ns chung là lười nên mk k muốn đánh máy, k hiểu thì ib lại vs mk)
c/ h(x) = 3x2 + 7x = 0
<=> x(3x + 7) = 0
<=> \(\left[{}\begin{matrix}x=0\\3x+7=0\Rightarrow3x=-7\Rightarrow x=\dfrac{-7}{3}\end{matrix}\right.\)
Vậy đa thức h(x) có 2 no là:....(tự ghi)

a, f(1) = 100 + 99 + ... + 2 + 1 + 1
=> f(x) = (100 + 1) . 100 : 2 + 1 "100 là số số hạng từ 1 -> 100"
=> f(x) = 4951
Hihi..
b, g(1) = 1 + 1 + 1 +...+ 1 + 1 (2016 số 1 theo cách lấy số mũ lớn nhất của x cộng thêm 1)
g(1) = 1 . 2016
g(1) = 2016
g(-1) = 1 + (-1) + (-1)2 + ... + (-1)2014 + (-1)2015
g(-1) = [ 1 + (-1)2 + ... + (-1)2014 ] + [ (-1) + (-1)3 + ... + (-1)2015 ]
g(-1) = [ 1 . 1008 ] + [ (-1) . 1008 ]
g(-1) = 1008 - 1008
g(-1) = 0
k nha!!
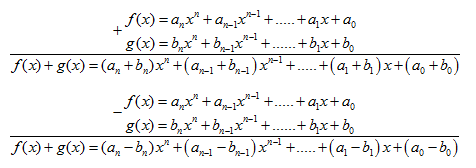
f(x) = anxn + an – 1xn– 1 + … + a1x + ao
-
g(x) = bnxn + bn – 1xn– 1 + … + b1x + bo
--------------------------------------------------------
f(x) - g(x) = (an - bn)xn + (an– 1 - bn – 1)xn– 1 + ..… + (a1 - b1)x + (ao - bo)