Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1.
Tạo với Ox là tạo với tia Ox hay trục hoành nhỉ? 2 cái này khác nhau đấy. Tạo với tia Ox thì chỉ có 1 góc 60 độ theo chiều dương, tạo với trục hoành thì có 2 góc 60 và 120 đều thỏa mãn. Coi như tạo tia Ox đi
Đường tròn tâm \(I\left(-2;-2\right)\) bán kính \(R=5\)
\(tan60^0=\sqrt{3}\Rightarrow\) tiếp tuyến có hệ số góc bằng \(\sqrt{3}\Rightarrow\) pt có dạng:
\(y=\sqrt{3}x+b\Leftrightarrow\sqrt{3}x-y+b=0\)
\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2\sqrt{3}+2+b\right|}{\sqrt{3+1}}=5\)
\(\Leftrightarrow\left|b+2-2\sqrt{3}\right|=10\Rightarrow\left[{}\begin{matrix}b=8+2\sqrt{3}\\b=-12+2\sqrt{3}\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}\sqrt{3}x-y+8+2\sqrt{3}=0\\\sqrt{3}x-y-12+2\sqrt{3}=0\end{matrix}\right.\)
\(d_1:2x+y-2-3\sqrt{5}=0\)
\(d_2:2x+y-2-3\sqrt{5}=0\)
\(d_3:y+1=0\)
\(d_4:4x-3y-9=0\)
Đáp án D
- Ta có :
(C1) tâm I1(0;2) và R1= 3; (C2) tâm I2( 3;-4) và R2= 3
- Nhận xét : 
không cắt C2
- Gọi d: ax+ by+ c= 0 là tiếp tuyến chung , thế thì : d(I1; d) = R1 và d (I2; d) = R2
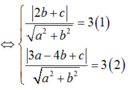
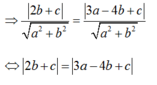
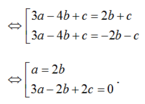
- Trường hợp: a= 2b thay vào (1):
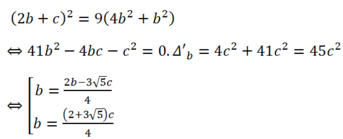
- Do đó ta có hai đường thẳng cần tìm :
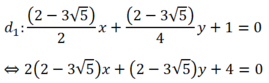
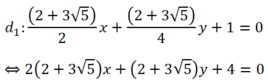
- Trường hợp :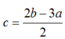 
thay vào :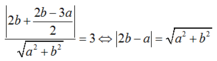 
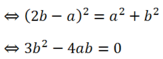
-Có 2 đường thẳng : d3: 2x- 1 = 0 và d4: 6x + 8y -1= 0.
Có tất cả 4 tiếp tuyến chung.
Đáp án B
- Ta có (C1) với tâm I(5; -12) và R= 15.
(C2) có tâm J( 1;2) và R’ =5 .
Gọi d là tiếp tuyến chung có phương trình: ax+ by+ c= 0 ().
- Khi đó ta có :
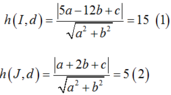
- Từ (1) và (2) suy ra :
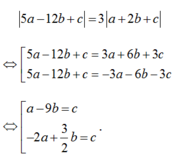
Thay vào (1):
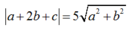
Ta có hai trường hợp :
- Trường hợp : c = a-9b thay vào (1):
(2a- 7b)2= 25 (a2+ b2)
hay 21a2+ 28ab -24b2= 0
Suy ra :
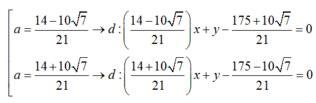
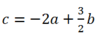
(1) => ( 7b- 2a)2=100(a2+b2) hay 96a2+ 28ab + 51b2= 0
Vô nghiệm.
Vậy 2 đường tròn đã cho có 2 tiếp tuyến chung.
a) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 3,b = 4,c = 21\)
Ta có \({a^2} + {b^2} - c = 9 + 16 - 21 = 4 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(3;4)\) và có bán kính \(R = \sqrt 4 = 2\)
b) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 1,b = - 2,c = 2\)
Ta có \({a^2} + {b^2} - c = 1 + 4 - 2 = 3 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(1; - 2)\) và có bán kính \(R = \sqrt 3 \)
c) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = \frac{3}{2},b = - 1,c = 7\)
Ta có \({a^2} + {b^2} - c = \frac{9}{4} + 1 - 7 = - \frac{{15}}{4} < 0\). Vậy đây không là phương trình đường tròn.
d) Phương trình không có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên phương trình đã cho không là phương trình đường tròn.
Giả sử phương trình tiếp tuyến có dạng:ax+by+c=0(a2+b2>0)
Từ gt =>(C1) có tâm O1(2;4) và bán kính 3 và (C2) có tâm O2(1;1) và bán kính 2.
khoảng cách từ O1 đến tiếp tuyến là:\(\frac{\left|2a+4b+c\right|}{\sqrt{a^2+b^2}}=3\left(1\right)\)
Tương tự ta có:\(\frac{\left|a+b+c\right|}{\sqrt{a^2+b^2}}=2\left(2\right)\)
Từ (1) và (2) =>2|2a+4b+c|=3|a+b+c|=>\(\left[{}\begin{matrix}c=a+5b\\c=\frac{-7a-11b}{5}\end{matrix}\right.\)
Thay vào (1) hoặc (2) ta có thể viết được a theo b hoặc b theo a rồi suy ra phương trình tương ứng