
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

\(A=\dfrac{2\sqrt{x}}{\sqrt{x}-4}-\dfrac{x+12\sqrt{x}}{x-16}\left(x\ge0;x\ne16\right)\\ A=\dfrac{2\sqrt{x}\left(\sqrt{x}+4\right)-x-12\sqrt{x}}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\\ A=\dfrac{2x+8\sqrt{x}-x-12\sqrt{x}}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+4}\)

xí câu 1:))
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\frac{x^2}{y-1}+\frac{y^2}{x-1}\ge\frac{\left(x+y\right)^2}{x+y-2}\)(1)
Đặt a = x + y - 2 => a > 0 ( vì x,y > 1 )
Khi đó \(\left(1\right)=\frac{\left(a+2\right)^2}{a}=\frac{a^2+4a+4}{a}=\left(a+\frac{4}{a}\right)+4\ge2\sqrt{a\cdot\frac{4}{a}}+4=8\)( AM-GM )
Vậy ta có đpcm
Đẳng thức xảy ra <=> a=2 => x=y=2

\(a_1,\sqrt{x}< 7\\ \Rightarrow x< 49\\ a_2,\sqrt{2x}< 6\\ \Rightarrow x< 18\\ a_3,\sqrt{4x}\ge4\\ \Rightarrow4x\ge16\\ \Rightarrow x\ge4\\ a_4,\sqrt{x}< \sqrt{6}\\ \Rightarrow x< 6\)
\(b_1,\sqrt{x}>4\\ \Rightarrow x>16\\ b_2,\sqrt{2x}\le2\\ \Rightarrow2x\le4\\ \Rightarrow x\le2\\ b_3,\sqrt{3x}\le\sqrt{9}\\ \Rightarrow3x\le9\\ \Rightarrow x\le3\\ b_4,\sqrt{7x}\le\sqrt{35}\\ \Rightarrow7x\le35\\ \Rightarrow x\le5\)

biểu thức căn trừ 2 phần x trừ 1 xác định khi
A x lớn hơn 1
B x lớn hơn hoặc bằng 1
C x bé hơn 1
D x bằng 1
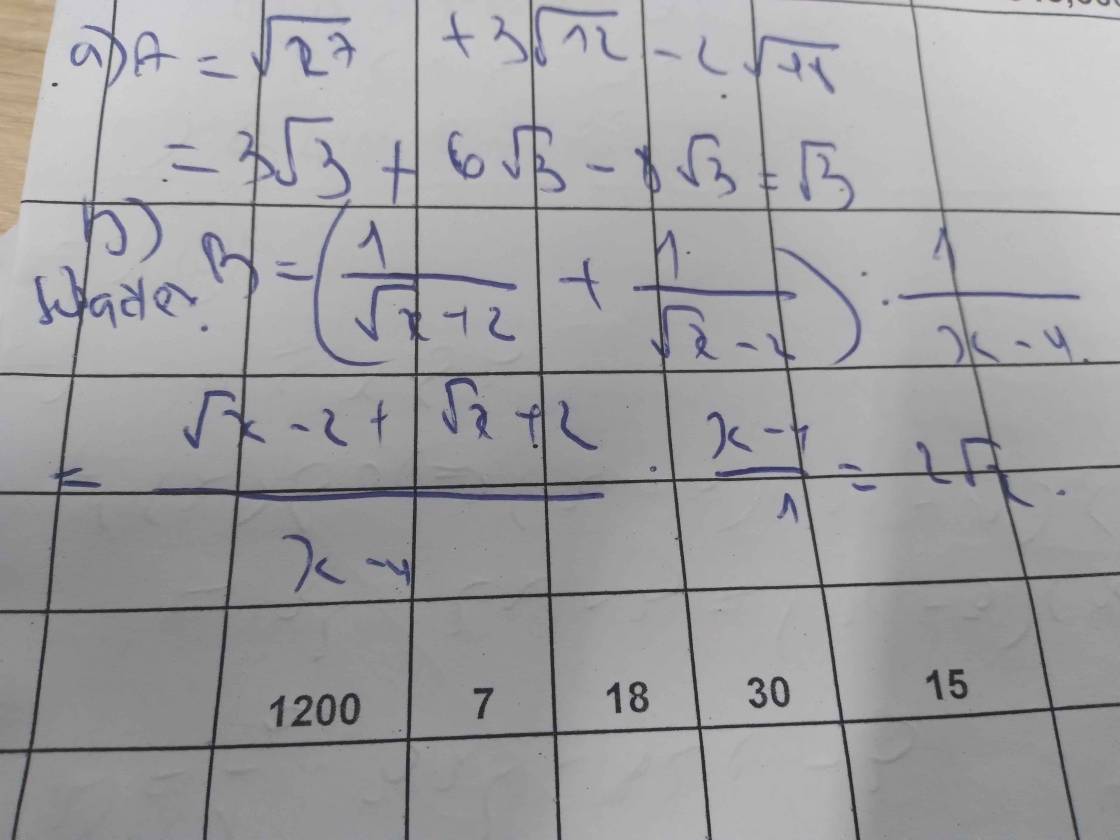
\(B=\dfrac{x+12}{\sqrt{x}+2}\) (điều kiện \(x\ge0\))
Đặt \(\sqrt{x}=t\left(t\ge0\right)\), khi đó \(B=\dfrac{t^2+12}{t+2}\) \(\Rightarrow\left(t+2\right)B=t^2+12\) \(\Leftrightarrow t^2-B.t+12-2B=0\) (*)
Phương trình (*) có \(\Delta=\left(-B\right)^2-4.1.\left(12-2B\right)\) \(=B^2+8B-48\)
Để pt (*) có nghiệm thì \(\Delta\ge0\) hay \(B^2+8B-48\ge0\) \(\Leftrightarrow\left(B+12\right)\left(B-4\right)\ge0\)
Ta xét 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}B+12\ge0\\B-4\ge0\end{matrix}\right.\Leftrightarrow B\ge4\)
TH2: \(\left\{{}\begin{matrix}B+12\le0\\B-4\le0\end{matrix}\right.\Leftrightarrow B\le-12\)
Ta thấy do \(x\ge0\) nên \(x+12>0\) và \(\sqrt{x}+2>0\). Do đó \(B>0\). Vậy trường hợp 2 \(\left(B\le-12\right)\) là không thể xảy ra. Vậy ta chỉ nhận trường hợp \(B\ge4\) hay \(min_B=4\)
Khi \(B=4\) thì thay vào (*), ta có \(t^2-4t+12-2.4=0\) \(\Leftrightarrow t^2-4t+4=0\) \(\Leftrightarrow\left(t-2\right)^2=0\) \(\Leftrightarrow t=2\) (nhận)
\(\Leftrightarrow\sqrt{x}=2\) \(\Leftrightarrow x=4\) (nhận)
Vậy \(B\ge4\). Dấu "=" xảy ra khi \(x=4\)