
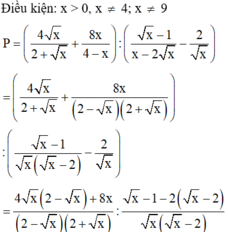
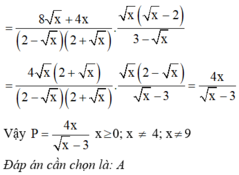
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

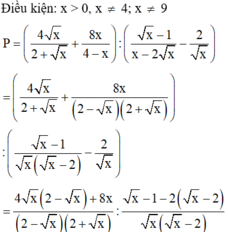
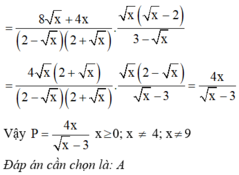

)1) \(x^2-9=x^2-3^2=\left(x-3\right)\left(x+3\right)\)
2) \(9x^2-16=\left(3x\right)^2-4^2=\left(3x-4\right)\left(3x+4\right)\)
3) \(x^2-5=x^2-\left(\sqrt{5}\right)^2=\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)\)
4) \(x-9=\left(\sqrt{x}\right)^2-3^2=\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\)(ĐK: \(x\ge0\))
5) \(x-3=\left(\sqrt{x}\right)^2-\left(\sqrt{3}\right)^2=\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)\)(ĐK: nt)
6) \(x+2\sqrt{x}+1=\left(\sqrt{x}\right)^2+2\cdot\sqrt{x}\cdot1+1=\left(\sqrt{x}+1\right)^2\)(ĐK: nt)
7) \(x-4\sqrt{x}+4=\left(\sqrt{x}\right)^2-2\cdot\sqrt{x}\cdot2+2^2=\left(\sqrt{x}-2\right)^2\)(ĐK: nt)
8) \(4x+4\sqrt{x}+1=\left(2\sqrt{x}\right)^2+2\cdot2\sqrt{x}\cdot1+1=\left(2\sqrt{x}+1\right)^2\)(ĐK:nt
9)
\(x+2\sqrt{x}-35\\ =x-5\sqrt{x}+7\sqrt{x}-35\\ =\sqrt{x}\left(\sqrt{x}-5\right)+7\left(\sqrt{x}-5\right)\\=\left(\sqrt{x}-5\right)\left(\sqrt{x}+7\right)\)(ĐK: nt)

\(a,\dfrac{x+2\sqrt{x}-3}{\sqrt{x}-1}\)
\(\Leftrightarrow\dfrac{x+3\sqrt{x}-\sqrt{x}-3}{\sqrt{x}-1}\)
\(\Leftrightarrow\dfrac{\sqrt{x}.\left(\sqrt{x}+3\right)-\left(\sqrt{x}+3\right)}{\sqrt{x}-1}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)
\(\Rightarrow\sqrt{x}+3\)
\(b,\dfrac{4y+3\sqrt{y}-7}{4\sqrt{y}+7}\)
\(\Leftrightarrow\dfrac{4y+7\sqrt{y}-4\sqrt{y}-7}{4\sqrt{y}+7}\)
\(\Leftrightarrow\dfrac{\sqrt{y}.\left(4\sqrt{y}\right)-\left(4\sqrt{y}+7\right)}{4\sqrt{y}+7}\)
\(\Leftrightarrow\dfrac{\left(4\sqrt{y}+7\right).\left(\sqrt{y}-1\right)}{4\sqrt{y}+7}\)
\(\Rightarrow\sqrt{y}-1\)
\(c,\dfrac{x\sqrt{y}-y\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
\(\Leftrightarrow\dfrac{\sqrt{xy}.\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}\)
\(\Rightarrow\sqrt{xy}\)
\(d,\dfrac{x-3\sqrt{x}-4}{x-\sqrt{x}-12}\)
\(\Leftrightarrow\dfrac{x+\sqrt{x}-4\sqrt{x}-4}{x+3\sqrt{x}-4\sqrt{x}-12}\)
\(\Leftrightarrow\dfrac{\sqrt{x}.\left(\sqrt{x}+1\right)-4\left(\sqrt{x}+1\right)}{\sqrt{x}.\left(x+3\right)-4\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}+1\right).\left(\sqrt{x}-4\right)}{\left(\sqrt{x}+3\right).\left(\sqrt{x}-4\right)}\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
\(\Rightarrow\dfrac{x-2\sqrt{x}-3}{x-9}\)
\(e,\dfrac{1+\sqrt{x}+\sqrt{y}+\sqrt{xy}}{1+\sqrt{4}}\)
\(\Leftrightarrow\dfrac{1+\sqrt{x}+\sqrt{y}+\sqrt{xy}}{1+2}\)
\(\Rightarrow\dfrac{1+\sqrt{x}+\sqrt{y}+\sqrt{xy}}{3}\)

\(A=\dfrac{x+8+\sqrt{x}+2}{x\sqrt{x}+8}+\dfrac{2-\sqrt{x}}{x-4}\)
\(=\dfrac{x+\sqrt{x}+10}{x\sqrt{x}+8}-\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+10-x+2\sqrt{x}-4}{\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)}=\dfrac{3\sqrt{x}+6}{\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)}\)
\(=\dfrac{3}{x-2\sqrt{x}+4}\)
Để A là số nguyên thì \(x-2\sqrt{x}+4\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow x-2\sqrt{x}+1=0\)
=>x=1

Lời giải:
a) \(A=4\sqrt{x}-\frac{(\sqrt{x}+3)^2(\sqrt{x}-3)}{x-9}=4\sqrt{x}-\frac{(\sqrt{x}+3)(x-9)}{x-9}=4\sqrt{x}-(\sqrt{x}+3)\)
\(=3\sqrt{x}-3\)
b)
\(B=\frac{\sqrt{9x^2+12x+4}}{3x+2}=\frac{\sqrt{(3x)^2+2.3x.2+2^2}}{3x+2}=\frac{\sqrt{(3x+2)^2}}{3x+2}=\frac{|3x+2|}{3x+2}\)
\(B=1\) nếu $x>\frac{-2}{3}$
$B=-1$ nếu $x< \frac{-2}{3}$

a) Ta có: \(x=9\)thỏa mãn đk
\(\Rightarrow\)Thay \(x=9\)vào biểu thức ta được:
\(A=\frac{3\sqrt{9}}{1-\sqrt{9}}=\frac{9}{-2}=\frac{-9}{2}\)
b) Với x thỏa mãn ĐKXĐ thì ta có:
\(B=\frac{1}{\sqrt{x}+2}-\frac{x+12}{4-x}-\frac{4}{\sqrt{x}-2}\)
\(=\frac{1}{\sqrt{x}+2}+\frac{x+14}{x-4}-\frac{4}{\sqrt{x}-2}\)
\(=\frac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\frac{x+12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\frac{4\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\left(\sqrt{x}-2\right)+\left(x+12\right)-4\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}-2+x+12-4\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{x-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\frac{\sqrt{x}-1}{\sqrt{x}+2}\)
1. x = 9 => A = \(\frac{3\sqrt{9}}{1-\sqrt{9}}=\frac{9}{-2}=-\frac{9}{2}\)
2. \(B=\frac{1}{\sqrt{x}+2}-\frac{x+12}{4-x}-\frac{4}{\sqrt{x}-2}=\frac{\sqrt{x}-2+x+12-4\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{x-3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\frac{x-\sqrt{x}-2\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\frac{\sqrt{x}-1}{\sqrt{x}+2}\)
3. \(AB>-\frac{3}{4}\) <=> \(\frac{3\sqrt{x}}{1-\sqrt{x}}\cdot\frac{\sqrt{x}-1}{\sqrt{x}+2}>-\frac{3}{4}\)
<=> \(-\frac{3\sqrt{x}}{\sqrt{x}+2}+\frac{3}{4}>0\)
<=> \(\frac{12\sqrt{x}-3\sqrt{x}-4}{4\left(\sqrt{x}+2\right)}< 0\)
<=> \(\frac{9\sqrt{x}-4}{4\sqrt{x}+8}< 0\)
Do \(4\sqrt{x}+8>0\)với mọi x => \(9\sqrt{x}-4< 0\) <=> \(x< \frac{16}{81}\)