Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: \(A=\dfrac{3}{n+2}\left(\forall n\in Z\right)\)
a) Để \(A\) là phân số thì \(n+2\ne0\Leftrightarrow n\ne-2\)
Vậy \(n\ne-2\) thì \(A\) là phân số.
b) Thay \(n=0;n=2;n=-7\) lần lượt vào \(A\) ta có:
\(\left\{{}\begin{matrix}A=\dfrac{3}{0+2}=\dfrac{3}{2}\\A=\dfrac{3}{2+2}=\dfrac{3}{4}\\A=\dfrac{3}{-7+2}=\dfrac{-3}{5}\end{matrix}\right.\)
c) Để \(A\in Z\Rightarrow\left(n+2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow n\in\left\{-1;-3;1;-5\right\}\)
Vậy \(n\in\left\{-1;-3;1;-5\right\}\) thì \(A\in Z\)
a) Điều kiện: \(n-4\ne0\Leftrightarrow n\ne4\)
Vậy \(\hept{\begin{cases}n\ne4\\n\inℤ\end{cases}}\)thì A là phân số
b) Với \(n\inℤ\):Để \(A\inℤ\)
\(\Leftrightarrow n-4\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
\(\Leftrightarrow n\in\left\{-3;3;7;11\right\}\)
Kết hợp ĐKXĐ .Vậy \(n\in\left\{-3;3;7;11\right\}\)thì \(A\inℤ\)
c)Với n=19 (thỏa mãn điều kiện) thì:
A=\(\frac{7}{19-4}=\frac{7}{15}\)
Với n=-17(thỏa mãn điều kiện) thì:
A=\(\frac{7}{-17-4}=\frac{7}{-21}=-\frac{1}{3}\)
a: Để A là phân số thì n-2<>0
=>n<>2
Khi n=-2 thì \(A=\dfrac{2\cdot\left(-2\right)+1}{-2-2}=\dfrac{-3}{-4}=\dfrac{3}{4}\)
b: Để A nguyên thì 2n+1 chia hết cho n-2
=>2n-4+5 chia hết cho n-2
=>\(n-2\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{3;1;7;-3\right\}\)
a) Số nguyên n phải: n-7 \(\inƯ\left(7\right)\)
b) Nếu n= -7 thì \(B=\frac{7}{-7}=-1\)
c) Muốn B nguyên thì n \(\in\left\{0;6;8;14\right\}\)
Ta có:\(A=\frac{5}{n-1}\left(n\in Z\right)\)
Mà phân số có mẫu là 0 thì phân số đó không xác định, vì vậy để A là phân số thì:
\(\Rightarrow\)ĐKXĐ: \(n-1\ne0\Leftrightarrow n\ne1\)
Để A nhận được giá trị nguyên thì 5 phải chia hết cho (n-1)
\(\Leftrightarrow\left(n-1\right)\in U\left(5\right)\)
\(\Rightarrow U\left(5\right)=\left\{1;-1;-5;5\right\}\)
Lập bảng kiểm tra
| n | 1 | -1 | 5 | -5 |
| n-1 | 0 | -2 | 4 | -6 |
\(\Rightarrow n\in\left\{-2;4;-6\right\}\)
a. điều kiện của n để B là phân số là :
\(n-2\ne0\Leftrightarrow n\ne2\)
b. ta có \(B=\frac{n-7}{n-2}=1-\frac{5}{n-2}\) nguyên khi n-2 là ước của 5
hay \(n-2\in\left\{-5;-1;1;5\right\}\Leftrightarrow n\in\left\{-3;1;3;7\right\}\)
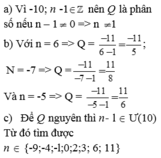
a) Để A là phân số thì \(n\ne-2\) ( Vì nếu \(n=-2\) thì mẫu số của A sẽ bằng 0 ⇒ A lúc đó sẽ không thể là phân số).
b) Để A là số nguyên ⇒7⋮\(n-2\)
\(7⋮n-2\\ \Rightarrow n-2\inƯ\left(7\right)\)
Mà \(Ư\left(7\right)=\left\{-7;-1;1;7\right\}\) ⇒ ta có bảng sau:
Vậy để A là số nguyên thì \(n\in\left\{-5;-1;3;9\right\}\)
a, A là phân số `<=> n-2 ne 0 <=> n ne 2.`
b, `7/(n-2) in ZZ <=> 7 vdots n-2.`
`<=> n-2 in Ư(7).`
`<=>` \(\left[{}\begin{matrix}n-2=1\\n-2=-1\\n-2=7\\n-2=-7\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}n=3\\n=1\\n=9\\n=-5\end{matrix}\right.\)
Vậy tập nghiệm của PT là: `S={-5; 1; 3; 9}`.