
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

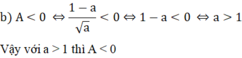

\(đkxđ\Leftrightarrow\hept{\begin{cases}a\ge0\\a\ne1\end{cases}}\)
\(A=\)\(\left(\frac{\sqrt{a}}{2}-\frac{1}{2\sqrt{a}}\right)^2\)\(\left(\frac{\sqrt{a}-1}{\sqrt{a}+1}-\frac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\left(\frac{\sqrt{a}.\sqrt{a}}{2\sqrt{a}}-\frac{1}{2\sqrt{a}}\right)^2\)\(\left(\frac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}-\frac{\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right)\)
\(=\left(\frac{a-1}{2\sqrt{a}}\right)^2\left(\frac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\frac{\left(a-1\right)^2}{\left(2\sqrt{a}\right)^2}\left(\frac{a-2\sqrt{a}+1-a-2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right)\)
\(=\frac{\left(a-1\right)^2.-4\sqrt{a}}{4a\left(a-1\right)}=\frac{a-1}{\sqrt{a}}\)
\(b,A< 0\Rightarrow\frac{a-1}{\sqrt{a}}< 0\)
Mà \(\sqrt{a}\ge0\Rightarrow a-1\le0\Rightarrow a\le1\)
\(A=2\Rightarrow\frac{a-1}{\sqrt{a}}=2\)
\(\Rightarrow a-1=2\sqrt{a}\Rightarrow a-2\sqrt{a}-1=0\)
\(\Rightarrow a-2\sqrt{a}+1-2=0\)
\(\Rightarrow\left(\sqrt{a}-1\right)^2-\sqrt{2}^2=0\)
\(\Rightarrow\left(\sqrt{a}-1-\sqrt{2}\right)\left(\sqrt{a}-1+\sqrt{2}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\sqrt{a}=1+\sqrt{2}\\\sqrt{a}=1-\sqrt{2}\end{cases}\Rightarrow\orbr{\begin{cases}a=\left(1+\sqrt{2}\right)^2=3+2\sqrt{2}\\a=\left(1-\sqrt{2}\right)^2=3-2\sqrt{2}\end{cases}}}\)
\(\left(\frac{\sqrt{a}}{2}-\frac{1}{2\sqrt{a}}\right)^2\left(\frac{\sqrt{a}-1}{\sqrt{a}+1}-\frac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\left(\frac{a-1}{2\sqrt{a}}\right)^2\left(\frac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}-\frac{\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right)\)
\(=\frac{\left(a-1\right)^2}{4a}.\frac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\frac{\left(a-1\right)^2}{4a}.\frac{\left(\sqrt{a}-1+\sqrt{a}+1\right)\left(\sqrt{a}-1-\sqrt{a}-1\right)}{a-1}\)
\(=\frac{a-1}{4a}.\frac{2\sqrt{a}.\left(-2\right)}{1}\)
\(=\frac{a-1}{4a}.\frac{-4\sqrt{a}.}{1}\)
\(=\frac{1-a}{\sqrt{a}}\)

a)A=\(\left(\frac{\sqrt{a}^2-1}{2\sqrt{a}}\right)^2\left(\frac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
=\(\left(\frac{a-1}{2\sqrt{a}}\right)^2\left(\frac{\left(\sqrt{a}-1+\sqrt{a}+1\right)\left(\sqrt{a}-1-\sqrt{a}-1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
=\(\left(\frac{a-1}{2\sqrt{a}}\right)^2\left(\frac{-4\sqrt{a}}{a-1}\right)\)
=\(\frac{a-1}{\sqrt{a}}\cdot\left(-1\right)\)
=\(\frac{1-a}{\sqrt{a}}\)
b) để A<0 thì (ĐKXĐ a#0 a#1
\(\frac{1-a}{\sqrt{a}}< 0\)
mà \(\sqrt{a}>0\)
=> 1-\(\sqrt{a}< 0\)
=> \(\sqrt{a}>1\)
=> a>1

Tự làm đi easy quá mà :)))) không biết quy đồng mà rút gọn hay sao

a) P = \(\left(\frac{\sqrt{a}}{2}-\frac{1}{2\sqrt{a}}\right)^2.\left(\frac{\sqrt{a}-1}{\sqrt{a}+1}-\frac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
P = \(\left(\frac{\sqrt{a}.\sqrt{a}-1}{2\sqrt{a}}\right)^2\cdot\frac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
P = \(\frac{\left(a-1\right)^2}{4a}\cdot\frac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{a-1}\)
P = \(\frac{a-1}{4\sqrt{a}^2}\cdot\left(-4\sqrt{a}\right)\)
P = \(\frac{1-a}{\sqrt{a}}\)
b) với x > 0 và x khác 1
P < 0 => \(\frac{1-a}{\sqrt{a}}< 0\)
Do \(\sqrt{a}>0\) => 1 - a < 0 => a > 1
Vậy S = {a|a > 1}
Có 1 kiểu hơi khác Conan 1 tí -.-
\(a)P=\left(\frac{\sqrt{a}.\sqrt{a}-1}{2\sqrt{a}}\right).\frac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\left(\frac{a-1}{2\sqrt{a}}\right)^2.\frac{a-2\sqrt{a}+1-a-2\sqrt{1}-1}{a-1}=\frac{\left(a-1\right)\left(-4\sqrt{a}\right)}{\left(2\sqrt{a}\right)^2}\)
\(=\frac{\left(1-a\right).4\sqrt{a}}{4a}=\frac{1-a}{\sqrt{a}}\)
Vậy \(P=\frac{1-a}{\sqrt{a}}\)với a > 0 và \(a\ne1\)
b) Do a > 0 và a khác 1 nên P < 0 khi và chỉ khi :
\(\frac{1-a}{\sqrt{a}}< 0\Leftrightarrow1-a< 0\Leftrightarrow a>1\)


\(p=\left(\frac{\sqrt{a}}{2}-\frac{1}{2\sqrt{a}}\right)^2.\left(\frac{\sqrt{a}-1}{\sqrt{a}+1}-\frac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\left(\frac{a-1}{2\sqrt{a}}\right)^2.\left(\frac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-1\right)-\left(\sqrt{a}+1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\frac{\left(a-1\right)^2}{\left(2\sqrt{a}\right)^2}.\frac{a-2a+1-a-2a-1}{\left(a-1\right)}\)
\(=\frac{\left(a-1\right)^2}{4a}.\frac{-4\sqrt{a}}{\left(a-1\right)}\)
\(=\frac{1-a}{\sqrt{a}}\)
\(b,\)Để P < 0 thì \(\frac{1-a}{\sqrt{a}}< 0\)
\(\sqrt{a}>0\)
\(1-a< 0\Rightarrow a>1\)
Vậy x > 1 thì P < 0