Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Ta có x =\(\frac{a}{y}\) và y =\(\frac{b}{z}\) (a;b là hằng số ≠≠ 0)
=> x=\(\frac{a}{b}\) = a: \(\frac{b}{z}\)= a . \(\frac{z}{b}\)=\(\frac{a}{b}\). z ( \(\frac{a}{b}\)à hằng số khác 0 )
Vậy x và z là tỉ lệ thuận theo hệ số tỉ lệ là abab
b,Ta có x và y là tỉ lệ nghịch , y và z là tỉ lệ thuận nên :
x= \(\frac{a}{y}\)(1) ; y =b.z (2) (a;b là hằng số khác 0)
Suy ra thay y theo z từ (2) vào (1)
x=\(\frac{a}{b.z}\) hay x.z = \(\frac{a}{b}\) (l\(\frac{a}{b}\)à hằng số khác 0 )
Vậy x và z là tỉ lệ nghịch với nhau theo hệ số tỉ lệ là \(\frac{a}{b}\)

|
Câu |
Đúng | Sai |
| a) Các số 7,5 và 12 là các ngọai tỉ | X | |
| b) Các số 4 và 7,5 là các trung tỉ | X | |
| c) Các số 4 và 22,5 là các trung tỉ | X | |
| d) Các số 22,5 và 12 là các trung tỉ | X | |
| e) Các số 7,5 và 22,5 là các ngoại tỉ | X |
| Câu | Đúng | Sai |
| a)Các số 7,5 và 12 là các ngoại tỉ | X | |
| b)Các số 4 và 7,5 là các trung tỉ | X | |
| c)Các số 4 và 22,5 là các trung tỉ | X | |
| d)Các số 22,5 và 12 là các trung tỉ | X | |
| e)Các số 7,5 và 22,5 là các ngoại tỉ | X |

Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ nghịch nên tích của chúng không đổi. Theo giá trị trong bảng thì $xy=2(-6)=-12$ (đây chính là công thức mô tả mối quan hệ phụ thuộc của x,y.
Ta có bảng:
| x | 2 | 4 | 5 | -4 | -1,2 | -24 |
| y | -6 | -3 | -2,4 | 3 | 10 | 0,5 |

a) Các ô trống trong bảng đều có cùng một giá trị là 7,8 vì
\(\dfrac{m}{V}=\dfrac{7,8}{1}=\dfrac{15,6}{2}=\dfrac{23,4}{3}=\dfrac{31,2}{4}=\dfrac{39}{5}=7,8\)
b) Vì \(\dfrac{m}{V}\) = 7,8 nên m= 7,8 V.
Vậy hai địa lượng m và V tỉ lệ thuận với nhau.
a) Các ô trống trong bảng đều có cùng một giá trị là 7,8 vì
mV=7,81=15,62=23,43=31,24=395=7,8mV=7,81=15,62=23,43=31,24=395=7,8
b) Vì \(\dfrac{m}{V}\)= 7,8 nên m= 7,8 V.
Vậy hai địa lượng m và V tỉ lệ thuận với nhau.

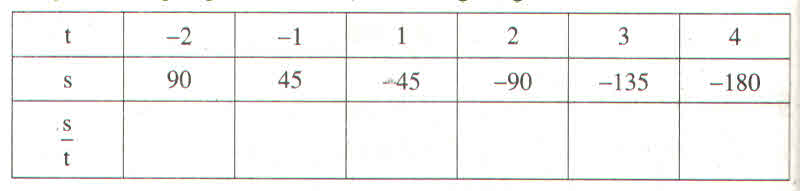
a)

b) s và t là hai đại lượng tỉ lệ thuận vì s = -45t
Hệ số tỉ lệ của s đối với t là -45

x | 2 | 4 | 5 | -4 | -1,2 | -24 |
y | -6 | -3 | -2,4 | 3 | 10 | 0,5 |
Vì x và y là hai đại lượng tỉ lệ nghịch, có x1y1 = 2.(-6) = -12 nên ta có công thức \(y = \dfrac{{ - 12}}{x}\).

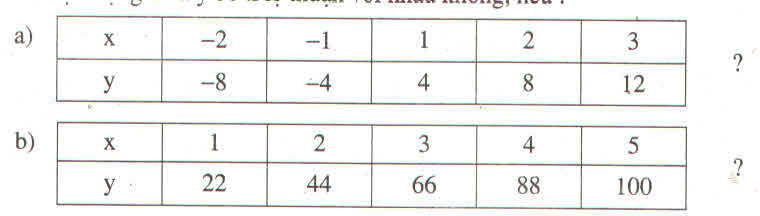
a)\(\dfrac{-8}{-2}=\dfrac{-4}{-1}=\dfrac{4}{1}=\dfrac{8}{2}=\dfrac{12}{3}=4\)
Vậy hai đại lượng x và y ở bảng a) tỉ lệ thuận với nhau.
b) \(\dfrac{22}{1}\ne\dfrac{100}{5}\)
Vậy hai đại lượng x và y ở bảng b không tỉ lệ thuận với nhau.



Vì x và y là hai đại lượng tỉ lệ nghịch nên xy = a (với a là một số khác 0).
Khi x = 2, y = 15 ⇒ a = xy = 30
Vì x và y là hai đại lượng tỉ lệ nghịch nên:
x1.y1 = x2.y2 = x3. y3 = x4.y4 = 30.
Kết quả như sau: