Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

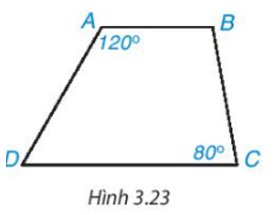
Để hình thang ABCD là hình thang cân thì \(\widehat A = \widehat B = {120^o};\widehat C = \widehat D = {80^o}\)
Suy ra \(\widehat A + \widehat B + \widehat C + \widehat D\)=120°+120°+80°+80°=400°>360°(không thỏa mãn định lí tổng bốn góc trong một tứ giác).
Khi đó, ABCD không phải là tứ giác.
Do đó ABCD cũng không phải là hình thang cân.

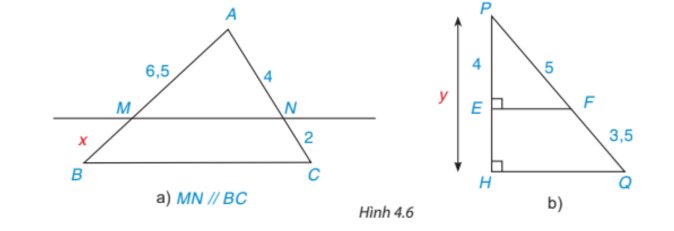
a)
Xét tam giác ABC có MN//BC
`=>(AM)/MB=(AN)/(NC)` (định lí thales)
`=>(6,5)/x=4/2`
`=>x=3,25`
b)
có QH⊥PH (hình vẽ)
FE⊥PH (hình vẽ)
Suy ra EF//HQ (từ vuông góc đến song song)
Xét tam giác PHQ có EF//HQ (cmt)
`=>(PE)/(PH)=(PF)/(PQ)` (định lí thales)
`=>4/x=5/(5+3,5)`
`=>4/x=5/(8,5)`
`=>x=6,8`

a)
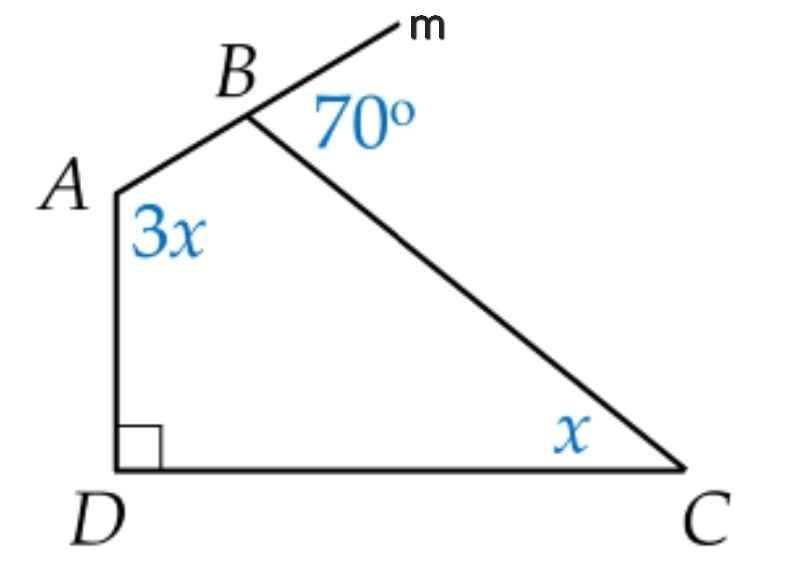 Ta có:
Ta có:
∠ABC + ∠CBm = 180⁰ (kề bù)
⇒ ∠ABC = 180⁰ - ∠CBm
= 180⁰ - 70⁰
= 110⁰
Tứ giác ABCD có:
∠A + ∠ABC + ∠C + ∠D = 360⁰ (tổng bốn góc trong tứ giác ABCD)
⇒ 3x + 110⁰ + x + 90⁰ = 360⁰
⇒ 4x + 200⁰ = 360⁰
⇒ 4x = 360⁰ - 200⁰
4x = 160⁰
⇒ x = 160⁰ : 4
⇒ x = 40⁰
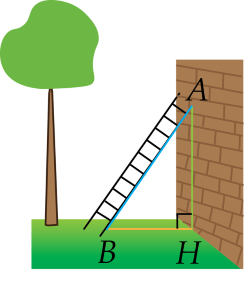
b) ∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 3,7² - 1,2²
= 12,25
⇒ AH = 3,5
⇒ AH/BH = 3,5/1,2 ≈ 2,9 > 2,2
Vậy thang cách chân tường không "an toàn"
a) Góc ngoài tại đỉnh \(B\) có số đo bằng \(7 0^{\circ}\) nên góc trong tại đỉnh \(B\) có số đo bằng \(18 0^{\circ} - 7 0^{\circ} = 11 0^{\circ}\)
Xét tứ giác \(A B C D ,\) ta có: \(\hat{A} + \hat{B} + \hat{C} + \hat{D} = 36 0^{\circ}\)
Do đó \(3 x + 11 0^{\circ} + x + 9 0^{\circ} = 36 0^{\circ}\)
uy ra \(4 x = 16 0^{\circ}\) nên \(x = 4 0^{\circ}\)
Vậy \(x = 4 0^{\circ}\).
b) Áp dụng định lí Pythagore vào tam giác \(A B H\) vuông tại \(H\) ta có: \(A B^{2} = A H^{2} + B H^{2}\)
Suy ra \(A H^{2} = A B^{2} - B H^{2}\)
Do đó \(A H = \sqrt{A B^{2} - B H^{2}} = \sqrt{3 , 7^{2} - 1 , 2^{2}} = 3 , 5\) m
Ta có \(\frac{A H}{B H} = \frac{3 , 5}{1 , 2} \approx 2 , 9\)
Mà \(2 , 9 > 2 , 2\) nên khoảng cách đặt thang cách chân tường đã cho là không an toàn.

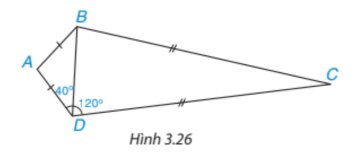
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

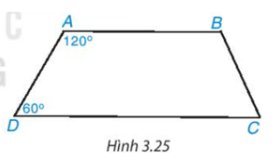
Do \(\widehat{A}+\widehat{D}=120^o+60^o=180^o\)
\(\Rightarrow AB//CD\)
\(\Rightarrow\) ABCD là hình thang.

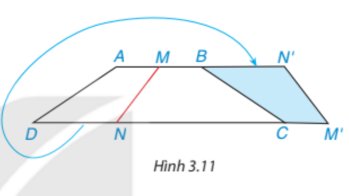
Ta cắt một mảnh giấy hình thang cân ABCD bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật hình thang AMND rồi ghép với hình thang MBCN dọc theo các cạnh bên của hình thang ban đầu, khi đó ta được một hình mới.
Tứ giác ABCD là hình thang cân nên AB // CD suy ra MN’ // M’N.
Do đó MN’M’N là hình thang.
Vì AB // CD nên \(\widehat {AMN} = \widehat {MNC}\) (2 góc so le trong)
Mà \(\widehat {AMN} = \widehat {CM'N'}\)(theo giả thiết)
\( \Rightarrow \widehat {MNC} = \widehat {CM'N}\)
Mà hai góc này là hai góc kề một đáy nên suy ra MN’M’N là hình thang cân.

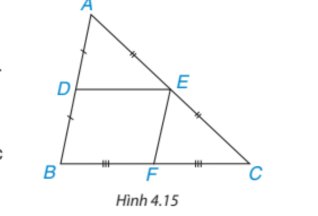
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).


Vì tứ giác ABCD là hình thang cân nên \(\widehat{ADC}=\widehat{BCD}\).
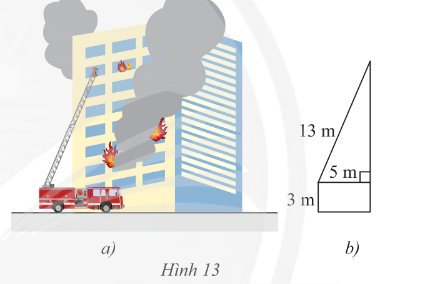




Gọi \(x\) là khoảng cách của xe đến đầu thang (m)
Áp dụng định lý Pythagore vào tam giác vuông trong hình ta có:
\({x^2} + {5^2} = {13^2}\)
\({x^2} = {13^2} - {5^2} = 144 = {12^2}\)
\(x = 12\) (m)
Chiều cao mà thang có thể vươn tới là:
\(12 + 3 = 15\) (m)