Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2

a) Vẽ đồ thị:
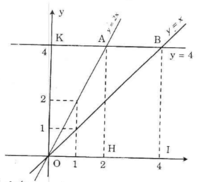
b) - Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4
=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)
- Tìm độ dài các cạnh của ΔOAB
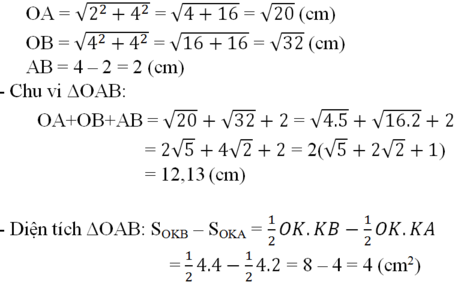
((*): muốn tìm tung độ hay hoành độ của một điểm khi đã biết trước hoành độ hay tung độ, ta thay chúng vào phương trình đồ thị hàm số để tìm đơn vị còn lại.)

a:
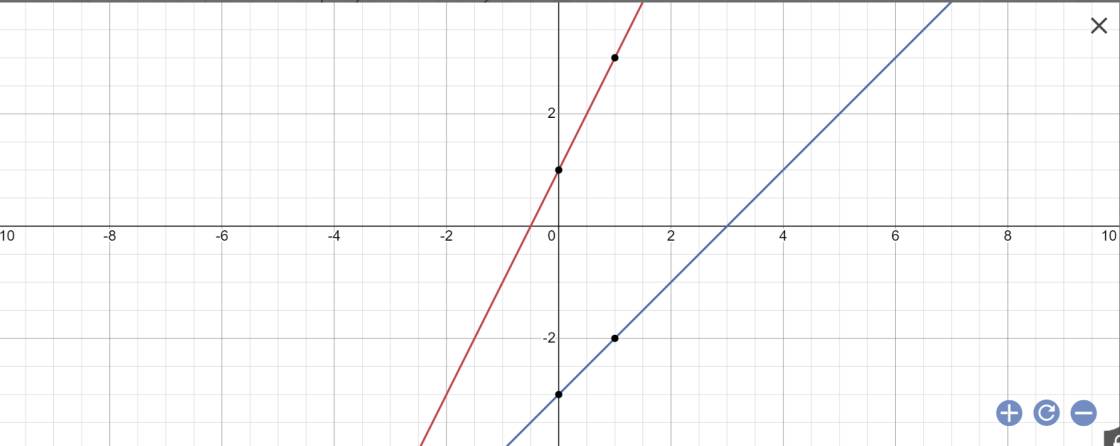
b: Phương trình hoành độ giao điểm là:
\(2x+1=x-3\)
=>\(2x-x=-3-1\)
=>x=-4
Thay x=-4 vào y=x-3, ta được:
\(y=-4-3=-7\)
Vậy: Tọa độ giao điểm của (D1) và (D2) là B(-4;-7)
c: Đặt phương trình đường thẳng (d3): y=ax+b
Vì (d3)//(d1) nên \(\left\{{}\begin{matrix}a=2\\b< >1\end{matrix}\right.\)
Vậy: y=2x+b
Thay x=1 và y=0 vào y=2x+b, ta được:
\(b+2\cdot1=0\)
=>b+2=0
=>b=-2
Vậy: (d): y=2x-2

b. Đồ thị đt đề cho là y=6
PTGD 2 đt đầu bài với đt câu b là: \(\left\{{}\begin{matrix}2x=6\\x-1=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\rightarrow A\left(3;6\right)\\x=7\rightarrow B\left(7;6\right)\end{matrix}\right.\)

b. PTHĐGĐ của hai hàm số:
\(x+2=-2x+1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
Thay x vào hs đầu tiên: \(y=-\dfrac{1}{3}+2=\dfrac{5}{3}\)
Tọa độ điểm \(A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)

Bạn tự vẽ nhé.
\(a,\) 2 đồ thị hàm số \(y=2x,y=-3x+5\) giao nhau khi và chỉ khi :
\(2x=-3x+5\\ \Leftrightarrow5x=5\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=2x\Leftrightarrow y=2\)
Vậy giao điểm của 2 đồ thị là \(\left(1;2\right)\)
\(b,\) 2 đồ thị hàm số \(y=3x+2,y=-\dfrac{1}{2}x+1\) giao nhau khi và chỉ khi :
\(3x+2=-\dfrac{1}{2}x+1\\ \Leftrightarrow\dfrac{7}{2}x=-1\\ \Leftrightarrow x=-\dfrac{2}{7}\)
Thay \(x=-\dfrac{2}{7}\) vào \(y=3x+2\Rightarrow y=\dfrac{8}{7}\)
Vậy giao điểm của 2 đồ thị là \(\left(-\dfrac{2}{7};\dfrac{8}{7}\right)\)
\(c,\) 2 đồ thị hàm số \(y=\dfrac{3}{2}x-2,y=-\dfrac{1}{2}x+2\) giao nhau khi và chỉ khi :
\(\dfrac{3}{2}x-2=-\dfrac{1}{2}x+2\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=2\)
Thay \(x=2\) vào \(y=\dfrac{3}{2}x-2\Rightarrow y=1\)
Vậy giao điểm của 2 đồ thị là \(\left(2;1\right)\)
\(d,\) 2 đồ thị hàm số \(y=-2x+5,y=x+2\) giao nhau khi và chỉ khi :
\(-2x+5=x+2\\ \Leftrightarrow-3x=-3\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=x+2\Rightarrow y=3\)
Vậy giao điểm của 2 đồ thị là \(\left(1;3\right)\)
chủ ngữ vị ngữ à