NQ
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
20 tháng 12 2016
bài 1
P= 5x2+2y2+4xy-4x+8y+25
= (4x2 +4xy+y2) + (x2-4x+4)+(y2 +8y +16)+5
= (2x+y)2+ (x-2)2+(y+4)2+5 lớn hơn hoặc bằng 5 với mọi x,y
dấu ''='' xảy ra <=> \(\begin{cases}2x+y=0\\x-2=0\\y+4=0\end{cases}\)
<=>\(\begin{cases}2x=-y\\x=2\\y=-4\end{cases}\)
<=> x= 2 và y =-4
vậy GTNN của P = 5 <=> x= 2 và y =-4
T
20 tháng 12 2016
câu 2
Giải 1.
Xét tứ giác ADHE có
góc DAE = góc ADH = góc AEH =90 độ (gt)
=> tứ giác ADHE là hình chứ nhật (dhnb)
Vậy tứ giác ADHE là hình chữ nhật
giải 2. giả sử AH cắt DE tại O . nối O với M
xét tam giác HEC vuông tại E( HE vuông góc với EC) có
EM là đường trung tuyến ứng với cạnh HC ( M là trung điểm HC)
=> EM = 1/2HC (t/c)
mà HM = 1/2 HC(M là trung điểm của HC)
=> EM=HM
Xét hình chữ nhật ADHE có : AH giao với DE tại O (gt)
=> O là trung điểm của AH và O là trung điểm DE (t/c)
mà AH=DE ( tứ giác ADHE là hình chữ nhật)
=> OH=OE
Xét tam giác OHM và tam giác OEM có
OH =OE(cmt)
HM= EM (cmt)
OM chung
do đó tam giác OHM = tam giác OEM (c-c-c)
=> góc OHM = góc OEM (2 góc tương ứng)
mà góc OHM=90 độ ( AH vuông góc với HC)=> góc OEM =90 độ hay góc DEM= 90 độ
Xét tam giác DEM có góc DEM 90 độ => tam giác DEM vuông tại E
Vậy tam giác DEM vuông tại E
giải 3: giải sử DE=2EM
mà DE= AH (cmt) và HC=2EM(cmt)
=> AH= HC
=> tam giác AHC cân tại H (dhnb) mà AHC=90 độ (AH vuông góc vs HC)
=> tam giác AHC vuông cân tại H ( dnhn)
=> góc ACH= 45 độ
Xét tam giác ABC vuông tại A có
góc ABC + góc ACB=90 độ (t/c)
=> góc ABC = 90độ - 45 độ = 45 độ
=>góc ABC = góc CAB
do đó tam giác ABC vuông cân (dhnb)
Vậy tam giác ABC vuông cân thì DE=2EM
US
16 tháng 12 2016
Ta có :
\(PT\Leftrightarrow2\sqrt{3x+1}-4+3-\frac{3}{\sqrt{2-x}}+2x-2=0\)
\(\Leftrightarrow\left(x-1\right)\left(\frac{6}{\sqrt{3x+1}+2}-\frac{3}{\sqrt{2-x}+1}+2\right)=0\)
( 1 )
Lại có : \(\frac{6}{\sqrt{3x+1}+2}-1>0\left(\frac{-1}{3}\le x< 2\right);3-\frac{3}{\sqrt{2-x}+1}>0\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra : \(PT\Leftrightarrow x=1\)
17 tháng 9 2021
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có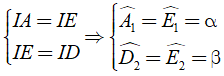
(vì trong tam giác, đối diện với hai cạn bằng
nhau là hai góc bằng nhau)
+ Xét tam giác ADE có
TD
17 tháng 9 2021
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có
26 tháng 3 2020
a.) Xét hai tg BEC và ACD có ^C chung, tg AHD vuông cân tại H (HD = HA) nên ^ADH = 45 độ suy ra
^ADC = 135 độ . Từ E vẽ thêm đường vuông góc AH tại K. Có tg AHB = tgEKA (vì AH = HD = KE, ^AEK = ^ACB = ^BAH) nên AB = AEVaayj tg BAE vuông cân tại A nên ^AEB = 45 độ suy ra ^BEC = 135 độ. Vậy ^BEC = ^ADC = 135 độ và ^C chung nên tg BEC và tam giác ADC đồng dạng.
Suy ra BE = AB.căn2 = m.căn2
b). Có AM = BE/2 (trung tuyến ứng cạnh huyền của tg vuôngBAE, DM = BE/2 trung tuyến ứng cạnh huyền của tg vuông BDE) vậy AM = MDHM chung AH = HD nên tgAHM = tgDHM(ccc) nên ^AHM =
^MHD = 45 độ suy ra ^BHM = 90 độ + 45 độ = 135 độ = ^BEC . Hay tg BHM và tgBEC có ^BHM = ^BEC, ^MBH chung nên hai tam giác BHM và BEC đồng dạng (gg) .
^AHM = 45 độ
c) AB=AE
=> tam giác ABE vuông cân
=> AG đồng thời là đường phân giác
=> GB/GC=AB/AC (t/c đường phân giác)(1)
tc ΔABC~ ΔHAC(g.g)
=> AB/AC=HA/HC (t/c...)(2)
từ 1 và 2 => GB/GC=HA/HC
HA=HD
~Học tốt!~
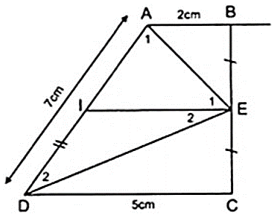
Theo bài ra ta có :
\(\frac{AB}{CD}=\frac{3}{4}\)(*) và \(CD=12\)cm
Thay \(CD=12\)vào (*) ta được :
\(\frac{AB}{12}=\frac{3}{4}=\frac{9}{12}\Leftrightarrow AB=9\)cm
Vậy AB = 9 cm
\(\frac{AB}{CD}\)=\(\frac{9}{12}\)