Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàng 1: (17+8)=5x5
Hàng 2: (13+7)=5x4
Hàng 3: (6+12)=6x3
Hàng 4: (10x6)=4x15
=> ?=15

Ta có:\(\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-y^3\)
với \(x=-10;y=2\) ,ta có:
\(\left(-10\right)^3-2^3=-1000-8=-1008\)
với \(x=-1;y=0\)
\(\left(-1\right)^3-0^3=-1-0=-1\)
với \(x=2;y=-1\) ,ta có:
\(2^3-\left(-1\right)^3=8-\left(-1\right)=8+1=9\)
với \(x=-0,5;y=1,25\), ta có:
\(\left(-0,5\right)^3-1,25^3=0-2=-2\)
Ta có bảng sau;
| Giá trị của x và y |
Giá trị của biểu thức \(\left(x-y\right)\left(x^2+xy+y^2\right)\) |
| \(x=-10;y=2\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1008\) |
| \(x=-1;y=0\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1\) |
| \(x=2;y=-1\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=9\) |
| \(x=-0,5;y=1,25\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-2\) |
Trước hết, ta làm tính nhân để rút gọn biểu thức, ta được:
(x - y)(x2 + xy + y2) = x . x2 + x . xy + x . y2 + (-y) . x2 + (-y) . xy + (-y) . y2
= x3 + x2y + xy2 – yx2 – xy2 – y3 = x3 – y3
Sau đó tính giá trị của biểu thức x3 – y3
Ta có:
Khi x = -10; y = 2 thì A = (-10)3 – 23 = -1000 – 8 = 1008
Khi x = -1; y = 0 thì A = (-1)3 – 03 = -1
Khi x = 2; y = -1 thì A = 23 – (-1)3 = 8 + 1 = 9
Khi x = -0,5; y = 1,15 thì
A = (-0,5)3 – 1,253 = -0,125 – 1.953125 = -2,078125

a. \(x^2-2xy+x^3y=x\left(x-2y+x^2y\right)\)
b. \(7x^2y^2+14xy^2-21^2y=7y\left(x^2y+2xy-63\right)\)
c. \(10x^2y+25x^3+xy^2=x\left(5x+y\right)^2\)

1a,(1-x)(x+2)=0
=>1-x=0=>x=1
=>x+2=0=>x=-2
1b,(2x-2)(6+3x)(3x+2)=0
=>2x-2=0=>2(x-1)=0=>x=1
=>6+3x=0=>3x=-6=>x=-2
=>3x+2=0=>3x=-2=>x=-2/3
1c,(5x-5)(3x+2)(8x+4)(x^2-5)=0
=>5x-5=0=>5(x-1)=0=>x=1
=>3x+2=0=>x=-2/3
=>8x+4=0=>4(2x+1)=0=>2x+1=0=>2x=-1=>x=-1/2
=>x^2-5=0=>x^2=5=>x=\(+-\sqrt{5}\)

Dùng hằng đẳng thức số 1 : (a + b)2 với a = (2x -1) và b =(x+1)
(2x - 1) 2 + 2(2x-1) (x+1) + (x+1)2 = (2x -1 + x +1)2 = (3x)2 = 9x2


a,
QUẢNG CÁO
b, Nhận xét:
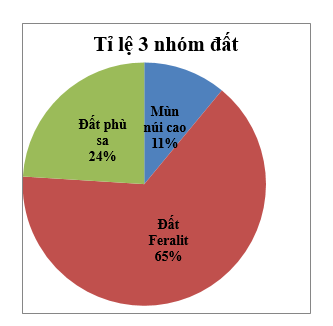
– Đất phù sa mới chủ yếu phân bố ở các đồng bằng: đồng bằng sông Hồng, đồng bằng sông Cửu Long và các đồng bằng Duyên hải miền Trung.
– Đất xám phân bố ở Đông Nam Bộ và phía tây Tây Nguyên.
– Đất pheralit badan tập trung nhiều nhất ở Tây Nguyên.
– Các loại đất pheralit khác và đất mùn núi cao có diện tích lớn nhâ’t và phân bô ở nhiều khu vực nước ta Trung du và miền núi Bắc Bộ, Ouyên hải Miền Trung, Tây Nguyên…
Cho bất phương trình - 4x + 12 > 0 . Phép biến đổi nào dưới đây đúng ?
- 4x + 12 < 0
<=> -4x < - 12
<=> 4x > 12
C
Khi x < 0 , kết quả rút gọn của biểu thức |- 4x| - 3x + 13 là :
\(\left|-4x\right|-3x+13=-4x-3x+13=-7x+13\)
=> D