Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
+) Vectơ \(\overrightarrow a \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \)
+) Vectơ \(\overrightarrow b \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \)
Suy ra giá của vectơ \(\overrightarrow a \) và vectơ \(\overrightarrow b \) song song với nhau nên \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Vậy khẳng định trên đúng
b) Giả sử vectơ \(\overrightarrow c \) có hướng từ A sang B
+) Vectơ \(\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
+) Vectơ \(\overrightarrow b \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
Suy ra, hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
Vậy khẳng định trên đúng
Khẳng định trên sai, chúng chỉ cùng phương, không cùng hướng.
a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ,
,
cùng phương với
=> ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
cùng phương với
=> ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ ,
cùng phương.
Vậy câu a) đúng.
b) Câu này cũng đúng.
Câu 5:
D. Các vector \(\overrightarrow{AB}, \overrightarrow{BA}, \overrightarrow{AC}, \overrightarrow{CA}, \overrightarrow{BC}, \overrightarrow{CB}\)
Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương nhưng chưa chắc là cùng hướng.
Chẳng hạn:
Khi A nằm giữa B và C thì hướng của vectơ \(\overrightarrow {AB} \) là từ phải sang trái, còn hướng của vectơ \(\overrightarrow {AC} \)là từ trái sang phải nên hai vectơ này là ngược hướng.
Tham khảo:
a) Đúng vì vectơ \(\overrightarrow 0 \) cùng hướng với mọi vectơ.
b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).
c) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì a // c và b // c do đó a // b tức là \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương , cùng chiều đo đó cùng hướng.
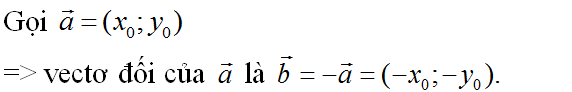
a) Gọi Δ1, Δ2, Δ3 lần lượt là giá của ba vectơ a→, b→, c→
+ Vectơ a cùng phương với vectơ c ⇒ Δ1 //≡ Δ3
+ Vectơ b cùng phương với vectơ c ⇒ Δ2 //≡ Δ3
⇒ Δ1 //≡ Δ2
⇒ Vectơ a→ cùng phương với b→ (theo định nghĩa).
b) a→, b→ cùng ngược hướng với c→
⇒ a→, b→ đều cùng phương với c→
⇒ a→ và b→ cùng phương.
⇒ a→ và b→ chỉ có thể cùng hướng hoặc ngược hướng.
Mà a→ và b→ đều ngược hướng với c→ nên a→ và b→ cùng hướng.