Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lần sau em đăng trong h.vn
1. \(log_{ab}c=\frac{1}{log_cab}=\frac{1}{log_ca+log_cb}=\frac{1}{\frac{1}{log_ac}+\frac{1}{log_bc}}=\frac{1}{\frac{log_ac+log_bc}{log_ac.log_bc}}=\frac{log_ac.log_bc}{log_ac+log_bc}\)
Đáp án B:
2. \(f'\left(x\right)=-4x^3+8x\)
\(f'\left(x\right)=0\Leftrightarrow-4x^3+8x=0\Leftrightarrow x=0,x=\sqrt{2},x=-\sqrt{2}\)
Có BBT:
x -căn2 0 căn2 f' f 0 0 0 - + - +
Nhìn vào bảng biên thiên ta có hàm số ... là đáp án C

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

a: \(\widehat{xOz}=80^0+20^0=100^0\)
b: \(\widehat{zOm}=\dfrac{\widehat{yOz}}{2}=10^0\)
\(\Leftrightarrow\widehat{xOm}=90^0\)

Đáp án C
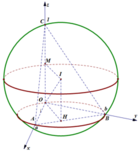
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y>0)
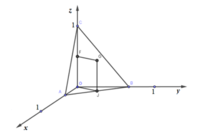
Vì OA+OB=OC = 1 => x+y=1
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G
Tam giác OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác
![]()
![]()
mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC=GO
=> GO=GA=GB=GC=> G là tâm mặt cầu ngoại tiếp tứ diện OABC.
Bán kính mặt cầu ngoại tiếp tứ diện OABC
![]()
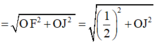
Ta có:
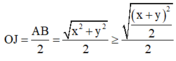
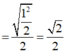
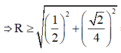
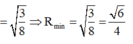

a) a = c, b = – d b) a = – c, b = d
c) a = d, b = c d) a = – c, b = – d

câu 5 ấy chắc thầy tui buồn ngủ nên quánh lộn chữ sai thành đúng r
12.
\(R=d\left(I;Oxz\right)=\left|y_I\right|=3\)
Phương trình:
\(x^2+\left(y+3\right)^2+z^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+6y=0\)
13.
\(R=d\left(M;\alpha\right)=\frac{\left|1-1+2.2-3\right|}{\sqrt{1^2+1^2+2^2}}=\frac{1}{\sqrt{6}}\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z+2\right)^2=\frac{1}{6}\)
14.
\(R=d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Phương trình:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z-1\right)^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y-2z-3=0\)


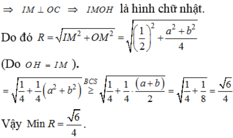
Chọn D
Tứ diện OABC có ba cạnh đôi một vuông góc không phải là hình chóp đều.