Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn điểm AA là điểm đầu thì chọn điểm cuối có 44 lựa chọn do →AA=⃗0AA→=0→
Tương tự chọn điểm BB là điểm đầu có 4 lựa chọn điểm cuối , chọn điểm CC là điểm đầu có 44 lựa chọn điểm cuối, chọn điểm DD là điểm đầu thì có 44 lựa chọn ở điểm cuối.
Vậy số vector khác vector không có điểm đầu và điểm cuối là các điểm đó là 4+4+4+4+4=204+4+4+4+4=20 vector.
Chọn điểm AA là điểm đầu thì chọn điểm cuối có 44 lựa chọn do →AA=⃗0AA→=0→
Tương tự chọn điểm B là điểm đầu có 4 lựa chọn điểm cuối , chọn điểm C là điểm đầu có 4 lựa chọn điểm cuối, chọn điểm D là điểm đầu thì có 44 lựa chọn ở điểm cuối.
Vậy số vector khác vector không có điểm đầu và điểm cuối là các điểm đó là 4+4+4+4+4=20 vector.

a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.

Số vecto khác vecto 0, có điểm đầu điểm cuối lấy từ 7 điểm A,B,C,D,E,F,O là:
\(A^2_7=7\cdot6=42\left(vecto\right)\)

Điểm đầu là A: `\vec(AB), \vec(AC),\vec(AD),\vec(AE)`
Điểm đầu là B: `\vec(BA),\vec(BC),\vec(BD),\vec(BE)`.

Tham khảo:
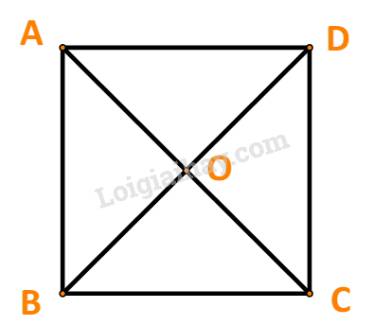
Tập hợp S là: \(S = \{ \overrightarrow {AB} ;\;\overrightarrow {AC} ;\;\overrightarrow {AD} ;\;\overrightarrow {AO} ;\;\overrightarrow {BA} ;\;\overrightarrow {BC} ;\;\overrightarrow {BD} ;\;\overrightarrow {BO} ;\;\overrightarrow {CB} ;\;\overrightarrow {CA} ;\;\overrightarrow {CD} ;\;\overrightarrow {CO} ;\;\overrightarrow {DB} ;\;\overrightarrow {DC} ;\;\overrightarrow {DA} ;\;\overrightarrow {DO} ;\;\overrightarrow {OB} ;\;\overrightarrow {OC} ;\;\overrightarrow {OD} ;\;\overrightarrow {OA} \} \)
Các nhóm trong S là:
\(\begin{array}{l}\{ \overrightarrow {AB} ;\overrightarrow {DC} \} ,\{ \overrightarrow {BA} ;\overrightarrow {CD} \} ,\{ \overrightarrow {AD} ;\overrightarrow {BC} \} ,\{ \overrightarrow {DA} ;\overrightarrow {CB} \} ,\\\{ \overrightarrow {AO} ;\overrightarrow {OC} \} ,\{ \overrightarrow {OA} ;\overrightarrow {CO} \} ,\{ \overrightarrow {OB} ;\overrightarrow {DO} \} ,\{ \overrightarrow {BO} ;\overrightarrow {OD} \} .\end{array}\)
Có 3 cách chọn điểm A
2 cách chọn điểm B
=> có 3.2=6 cách chọn vecto có điểm đầu và điểm cuối là 2 điểm trong 3 điểm pb A,B,C