DN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 4 2023
a: \(B=\dfrac{3x\left(2x-3\right)-4\left(2x+3\right)-4x^2+23x+12}{\left(2x-3\right)\left(2x+3\right)}\cdot\dfrac{2x+3}{x+3}\)
\(=\dfrac{6x^2-9x-8x-12-4x^2+23x+12}{2x-3}\cdot\dfrac{1}{x+3}\)
\(=\dfrac{2x^2+6x}{\left(2x-3\right)}\cdot\dfrac{1}{x+3}=\dfrac{2x}{2x-3}\)
b: 2x^2+7x+3=0
=>(2x+3)(x+2)=0
=>x=-3/2(loại) hoặc x=-2(nhận)
Khi x=-2 thì \(A=\dfrac{2\cdot\left(-2\right)}{-2-3}=\dfrac{-4}{-7}=\dfrac{4}{7}\)
d: |B|<1
=>B>-1 và B<1
=>B+1>0 và B-1<0
=>\(\left\{{}\begin{matrix}\dfrac{2x+2x-3}{2x-3}>0\\\dfrac{2x-2x+3}{2x-3}< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3< 0\\\dfrac{4x-3}{2x-3}>0\end{matrix}\right.\Leftrightarrow x< \dfrac{3}{4}\)
NT
25 tháng 8 2021
Ta có \(A=\dfrac{4x-3}{x+2}=\dfrac{4x+8-11}{x+2}=4-\dfrac{11}{x+2}\)
Để \(A\) nguyên thì \(11⋮\left(x+2\right)\Rightarrow\left(x+2\right)\inƯ\left(11\right)=\left\{1;-1;11;-11\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x+2=1\\x+2=-1\\x+2=11\\x+2=-11\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-3\\x=9\\x=-13\end{matrix}\right.\)
Vậy tất cả các x thỏa ycbt là x=-1;x=-3;x=9 hoặc x=-13
26 tháng 8 2021
Để A là số nguyên thì \(4x-3⋮x+2\)
\(\Leftrightarrow-11⋮x+2\)
\(\Leftrightarrow x+2\in\left\{1;-1;11;-11\right\}\)
hay \(x\in\left\{-1;-3;9;-13\right\}\)
PT
2
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Bài 4:
a. Ta thấy: $x^2-x+2=(x-\frac{1}{2})^2+1,75>0$ với mọi $x$.
Do đó để $B=\frac{x^2-x+2}{x-3}<0$ thì $x-3<0$
$\Leftrightarrow x<3$
b.
$B=\frac{x(x-3)+2(x-3)+8}{x-3}=x+2+\frac{8}{x-3}$
Với $x$ nguyên, để $B$ nguyên thì $x-3$ phải là ước của 8.
$\Rightarrow x-3\in\left\{\pm 1; \pm 2; \pm 4; \pm 8\right\}$
$\Rightarrow x\in \left\{4; 2; 5; 1; -1; 7; 11; -5\right\}$
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Bài 5:
\(\frac{\frac{x}{x-y}-\frac{y}{x+y}}{\frac{y}{x-y}+\frac{x}{x+y}}=\frac{\frac{x(x+y)-y(x-y)}{(x-y)(x+y)}}{\frac{y(x+y)+x(x-y)}{(x-y)(x+y)}}\)
\(=\frac{x(x+y)-y(x-y)}{y(x+y)+x(x-y)}=\frac{x^2+y^2}{x^2+y^2}=1\)
M
0
19 tháng 12 2021
Để A là số nguyên thì \(2x-1\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{1;0;3;-2\right\}\)
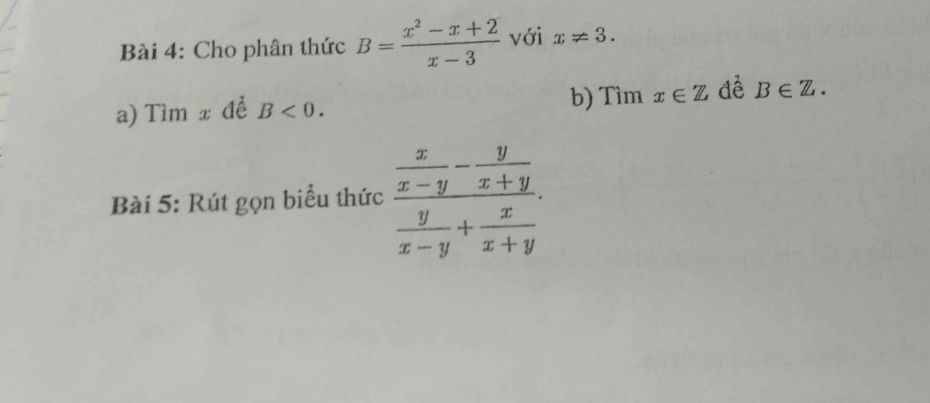
Có ai giúp mình với
Để B nguyên thì \(x-3\in\left\{1;-1;13;-13\right\}\)
hay \(x\in\left\{4;2;16;-10\right\}\)