LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PM
0
12 tháng 3 2017
Để \(B=\frac{1}{2\left(n-1\right)^2+3}\) đạt GTLN <=> \(2\left(n-1\right)^2+3\) đạt GTNN
Vì \(\left(n-1\right)^2\ge0\forall n\)
\(\Rightarrow2\left(n-1\right)^2\ge0\forall n\)
\(\Rightarrow2\left(n-1\right)^2+3\ge3\forall n\) có GTNN là 3
Dấu "=" xảy ra <=> \(2\left(n-1\right)^2=0\Rightarrow n=1\)
\(\Rightarrow B_{max}=\frac{1}{3}\) tại x = 1
3 tháng 10 2015
De B lon nhat
=> 2(n-1)2+3 nho nhat
Vi 2(n-1)2\(\ge\)0 => (n-1)2\(\ge0\)=> \(n\ge1\)
=> 2(n-1)2+3\(\ge3\)
=> Min B =3 khi n=1
K
5 tháng 6 2019
....
a) \(n\in\left(-1,1,3,5\right)\)thì A có giá trị nguyên
b) Ko hiểu
***
5 tháng 6 2019
A=n+1n−2n+1n−2
a. để B là phân số thì n-2 khác 0 => n khác 2
b.A=n+1n−2n+1n−2= n−2+3n−2n−2+3n−2= n−2n−2n−2n−2+3n−23n−2=1+3n−23n−2
để B nguyên khi n-2 là ước của 3
ta có ước 3= (-1;1;3;-3)
nên n-2=1=> n=3
n-2=-1=> n=1
n-2=3=> n=5
n-2=-3=> n=-1
vậy để A nguyên thì n=(-1;1;3;5)
16 tháng 1 2019
a.
Ta có:
(x+2)/327+(x+3)/326+(x+4)/325+(x+5)/324+(x+349)/5=0
<=>(x+2)/327+(x+3)/326+(x+4)/325+(x+5)/324+(x+329)-4 (giải thích: (x+349)/5=(x+329+20)/5=(x+329)/5+4)
<=>1+(x+2)/327+1+(x+3)/326+1+(x+4)/325+1+(x+5)324+(x+329)/5=0
<=>(x+329)/327+(x+329)/326+(x+329)/325+(x+329)/324+(x+329)/5=0
<=>x+329(1/327+1/326+1/325+1/324+1/5)=0
Vì (1/327+...+1/5) khác 0 => x+329=0
=>x=-329
31 tháng 5 2018
Bài 1:
a) ta có: \(A=\frac{2n-1}{n-3}=\frac{2n-6+5}{n-3}=\frac{2.\left(n-3\right)+5}{n-3}=\frac{2.\left(n-3\right)}{n-3}+\frac{5}{n-3}\)\(=2+\frac{5}{n-3}\)
Để A có giá trị nguyên
\(\Rightarrow\frac{5}{n-3}\in z\)
\(\Rightarrow5⋮n-3\Rightarrow n-3\inƯ_{\left(5\right)}=\left(5;-5;1;-1\right)\)
nếu n-3 = 5 => n = 8 (TM)
n-3 = -5 => n= -2 (TM)
n-3 = 1 => n = 4 (TM)
n-3 = -1 => n = 2 (TM)
KL: \(n\in\left(8;-2;4;2\right)\)
b) ta có: \(A=2+\frac{5}{n-3}\) ( pa)
Để A đạt giá trị lớn nhất
=> \(\frac{5}{n-3}\le5\)
Dấu "=" xảy ra khi
\(\frac{5}{n-3}=5\)
\(\Rightarrow n-3=5:5\)
\(n-3=1\)
\(n=4\)
KL: n =4 để A đạt giá trị lớn nhất
Bài 2 bn làm tương tự nha!
16 tháng 7 2021
a) A = \(\dfrac{6n+7}{2n+3}\) = \(\dfrac{6n+9}{2n+3}\) − \(\dfrac{2}{2n+3}\) nguyên
⇔ 2n + 3 ∈ Ư(2) = {-2; -1; 1; 2}
⇔ 2n ∈ {-5; -4; -2; -1}
Vì n nguyên nên n ∈ {-2; -1}
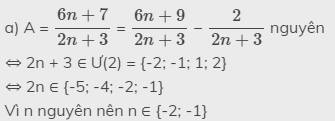
Ta có:
B=1/(2.(n-1)^2 +3)
Mà: (n-1)^2 > hoặc =0 <=>2(n-1)^2 > hoặc = 0 (dấu = xảy ra khi n=1)
Vậy ta dễ dàng suy ra 2(n-1)^2 +3 lớn hơn hặc =3
Để B đạt g trị lớn nhất thì mẫu phải đạt g trị nhỏ nhất, vậy Min 2(n-1)^2 +3 =3
Vậy ta có với n=1 thì B đạt giá trị nhỏ nhất và giá trị đó =1/3