Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(A=\dfrac{1.3-26}{2.6}-\left(\dfrac{1}{2}+\dfrac{1}{8}\right)\)
\(=\dfrac{-19}{2}-\dfrac{3}{8}=\dfrac{-79}{8}\)
\(B=\left(5+\dfrac{7}{8}-2-\dfrac{1}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}=\dfrac{13}{12}\)
b: Vì A<x<B nên \(\dfrac{-79}{8}< x< \dfrac{13}{12}\)
hay \(x\in\left\{-9;-8;...;0;1\right\}\)

a: \(A=\dfrac{1.3-2.6}{2.6}-\dfrac{5}{6}:2=\dfrac{-1}{2}-\dfrac{5}{12}=\dfrac{-11}{12}\)
\(B=\left(\dfrac{47}{8}-\dfrac{9}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}=\dfrac{47-18-4}{8}\cdot\dfrac{26}{75}=\dfrac{25}{75}\cdot\dfrac{26}{8}=\dfrac{13}{12}\)
b: Để A<x<B thì -11/12<x<13/12
mà x là số nguyên
nên \(x\in\left\{0;1\right\}\)

a: \(A=\dfrac{1.3-2.6}{2.6}-\dfrac{5}{6}:2=\dfrac{-1}{2}-\dfrac{5}{12}=\dfrac{-11}{12}\)
\(B=\left(\dfrac{47}{8}-\dfrac{9}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}\)
\(=\dfrac{47-18-4}{8}\cdot\dfrac{26}{75}=\dfrac{25}{75}\cdot\dfrac{26}{8}=\dfrac{1}{3}\cdot\dfrac{13}{4}=\dfrac{13}{12}\)
b: Để A<x<B thì \(\dfrac{-11}{12}< x< \dfrac{13}{12}\)
mà x là số nguyên
nên \(x\in\left\{0;1\right\}\)

a: \(A=\dfrac{1.3-2.6}{2.6}-\dfrac{5}{6}\cdot\dfrac{1}{2}=\dfrac{-1}{2}-\dfrac{5}{12}=\dfrac{-11}{12}\)
\(B=\left(\dfrac{22}{3}-\dfrac{9}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}=\dfrac{55}{12}\cdot\dfrac{26}{75}=\dfrac{143}{90}\)
b: Để A<x<B thì \(\dfrac{-11}{12}< x< \dfrac{143}{90}\)
mà x là số nguyên
nên \(x\in\left\{0;1\right\}\)

\(M=\left|x-2002\right|+\left|x-2001\right|\)\(=\left|x-2002\right|+\left|2001-x\right|\ge\left|x-2002+2001-x\right|=\left|-2002+2001\right|=1\)
tức \(M\ge1\) \(\Leftrightarrow\left[{}\begin{matrix}x-2001=0\\x-2002=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2001\\x=2002\end{matrix}\right.\)
Vậy MinM = - 1 \(\Leftrightarrow\left[{}\begin{matrix}x=2001\\x=2002\end{matrix}\right.\)

a: \(A=\dfrac{1.3-26}{2.6}-\dfrac{3}{8}\cdot\dfrac{1}{2}=-\dfrac{19}{2}-\dfrac{3}{16}=-\dfrac{155}{16}\)
b: \(B=\left(\dfrac{47}{8}-\dfrac{9}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}\)
\(=\dfrac{47-18-4}{8}\cdot\dfrac{26}{75}=\dfrac{1}{3}\cdot\dfrac{13}{4}=\dfrac{13}{12}\)
c: Để A<x<B thì \(-\dfrac{155}{16}< x< \dfrac{13}{12}\)
=>-10<x<2
hay \(x\in\left\{-9;-8;-7;...;0;1\right\}\)
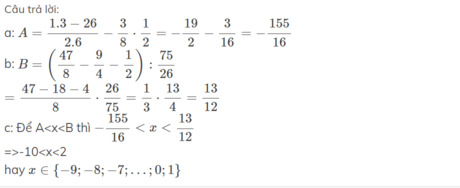
a.
\(A=\dfrac{1,11+0,19-13,2}{2,06+0,54}-\left(\dfrac{1}{2}+\dfrac{1}{4}\right):2\\ =\dfrac{2.2-13,2}{2,6}-\dfrac{3}{4}:2\\ =\dfrac{-11}{2,6}-\dfrac{3}{8}\\ =-\dfrac{55}{13}-\dfrac{3}{8}=-\dfrac{479}{104}\simeq-4,6\\ B=\left(5\dfrac{7}{8}-2\dfrac{1}{4}-0,5\right):2\dfrac{23}{26}\\ =\left(\dfrac{47}{8}-\dfrac{9}{4}-\dfrac{1}{2}\right):2\dfrac{23}{26}\\ =\dfrac{13}{12}=1.08\left(3\right)\)