K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 12 2023
a: Xét ΔABC có DE//BC
nên \(\dfrac{AE}{EC}=\dfrac{AD}{DB}\)
=>\(\dfrac{AD}{8}=\dfrac{3}{4}\)
=>\(AD=8\cdot\dfrac{3}{4}=6\)
AB=AD+BD
=>AB=6+8=14
b: Xét ΔABC có DE//BC
nên \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
mà \(\dfrac{AD}{DB}=\dfrac{EC}{AE}\)
nên \(\dfrac{AE}{EC}=\dfrac{EC}{AE}\)
=>\(AE^2=EC^2\)
=>AE=EC
=>E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
ED//BC
Do đó: D là trung điểm của AB
9 tháng 12 2023
a) Ta có AB // BC, nên theo định lí đường thẳng song song, ta có:
AE/EC = AB/BC = AB/DB (vì DB = BC)
Với AE/EC = 3/4, ta có:
3/4 = AB/DB
AB = (3/4) * DB = (3/4) * 8 = 6
b) Ta biết rằng D là trung điểm của AB, nên AD = DB/2 = 8/2 = 4.
Tương tự, E là trung điểm của AC, nên AE = EC/2.
Ta cần chứng minh rằng AD/DB = EC/AE.
Ta có:
AD/DB = 4/8 = 1/2
EC/AE = 2 * EC/2 * AE = 2 * EC/2 * (EC/2) = EC^2/(2 * AE)
Vì AE/EC = 3/4, nên AE = (3/4) * EC.
Thay vào biểu thức trên, ta có:
EC/AE = EC^2/(2 * (3/4) * EC) = EC/2
Vậy ta có AD/DB = EC/AE.
NT
1
LH
4 tháng 10 2017
Vì AD = DB , AE = AC
=> DE là đường trung bình của tam giác ABC
DE = 1/2 BC
DE = 1/2.8
DE = 4 (cm)
E
0
10 tháng 12 2023
a: Xét ΔABC có DE//BC
nên \(\dfrac{AE}{EC}=\dfrac{AD}{DB}\)
=>\(\dfrac{AD}{8}=\dfrac{3}{4}\)
=>\(AD=8\cdot\dfrac{3}{4}=6\left(cm\right)\)
AB=BD+AD
=6+8
=14(cm)
b: Xét ΔABC có DE//BC
nên \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
mà \(\dfrac{AD}{DB}=\dfrac{EC}{AE}\)
nên \(\dfrac{AE}{EC}=\dfrac{EC}{AE}\)
=>\(AE^2=EC^2\)
=>AE=EC
=>E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
ED//BC
Do đo: D là trung điểm của AB
TL
1
1 tháng 8 2019
Ta có: D là trung điểm của AB (AD = DB)
E là trung điểm của AC (AE = EC)
=> DE là đg trung bình cua tg ABC
=> DE // BC và DE = \(\frac{1}{2}\).BC
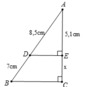
Xét ΔABC có DE//BC
nên AE/x=AD/DB
=>5.1/x=8.5/7
hay x=4,2(cm)
Ta có:\(DE\perp AC,BC\perp AC\Rightarrow\) DE//BC
Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\\ \Rightarrow\dfrac{8,5}{7}=\dfrac{5,1}{x}\\ \Rightarrow x=4,2\left(cm\right)\)