Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\) (3)
\(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \) (1)
TH1:
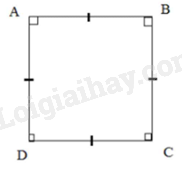
Nếu \(AB = BC\) (gt) thì \(AB = BC = CD = DA\) (2)
Từ (1), (2) suy ra \(ABCD\) là hình vuông
TH2:
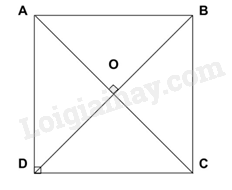
Nếu \(AC\) vuông góc với \(BD\)
Mà \(ABCD\) cũng là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (4)
Từ (1) và (4) suy ra \(ABCD\) là hình vuông
TH3:
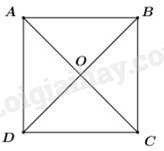
\(AC\) là phân giác của góc \(BAD\)
Mà \(ABCD\) là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (5)
Từ (1) và (5) suy ra \(ABCD\) là hình vuông

a) ABCD là hình bình hành
\(\Rightarrow\)AB // CD
\(\Rightarrow\)\(\widehat{BAC}\)= \(\widehat{ACD}\) (slt)
AD là phân giác \(\widehat{BAC}\)\(\Rightarrow\)\(\widehat{DAC}\)= 1/2 \(\widehat{BAC}\)
CK là phân giác \(\widehat{ACD}\)\(\Rightarrow\)\(\widehat{ACK}\)= 1/2 \(\widehat{ACD}\)
suy ra: \(\widehat{DAC}\) = \(\widehat{ACK}\)
mà \(\widehat{DAC}\)và \(\widehat{ACK}\) ở vị trí so le trong
\(\Rightarrow\)AE // CK
b) Gọi O là giao điểm của AC và BD (1)
\(\Rightarrow\)OA = OC
Xét \(\Delta BAE\)và \(\Delta DCK\)có
\(\widehat{KDC}\)= \(\widehat{EBA}\) (GT)
AB = CD (GT)
\(\widehat{KCD}\)= \(\widehat{EAB}\) (theo phần a)
suy ra \(\Delta BAE\) = \(\Delta DCK\)
\(\Rightarrow\)AE = CK
mà AE // CK
\(\Rightarrow\)AECK là hình bình hành
mà OA = OC
\(\Rightarrow\)AC và EK cắt nhau tại O (2)
Từ (1) và (2) \(\Rightarrow\)BD, AC, EK đồng quy

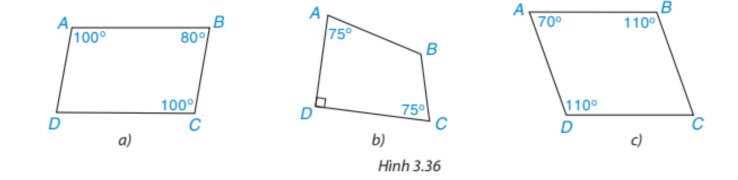
* Hình 3.36a)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
100°+80°+100°+\(\widehat D = {360^o}\)
280°+\(\widehat D\)=360°
Suy ra \(\widehat D\)=360°−280°=80°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=100°; \(\widehat B = \widehat D\)=80°
Do đó, tứ giác ABCD là hình bình hành.
* Hình 3.36b)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
75°+\(\widehat B\)+75°+90°=360°
240°+\(\widehat B\)=360°
Suy ra \(\widehat B\)=360°−240°=120°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=100° nhưng \(\widehat B \ne \widehat D\)(120°≠90°)
Do đó, tứ giác ABCD không là hình bình hành.
* Hình 3.36c)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
70°+110°+\(\widehat C\)+110°=360°
\(\widehat C\)+290°=360o
Suy ra \(\widehat C\)=360°−290°=70°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=70°; \(\widehat B = \widehat D\)=110°
Do đó, tứ giác ABCD là hình bình hành.
Vậy tứ giác ABCD trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác ABCD trong Hình 3.36b) không là hình bình hành.

b1 a) goi I la giao diem cua AD va BC
I A B C D
vi AB//DC => goc IDC = goc DAB (2 goc dong vi)
ma goc A =30 => goc IDC =30
lai co goc IDC + goc ADC =180 ( I,D,A thang hang)
30+ goc ADC =180 => goc ADC=150
vi AB//DC => goc ICD = goc CBA (2 goc dong vi)
có goc ICD+ goc DCB =180 (I,C,B thang hang )
goc ICD+ 120=180 => goc ICD = 60 => goc ABC=60
còn ý b) bạn làm tương tự nhé
b2
A B C D
vi DC =BC (gt) => tam giac DCB can tai C => goc CDB = goc DBC (1)
vi DB la phan giac cua goc ADC => g ADB =g BDC (2)
tu (1,2) => g ADB = g DBC
ma 2 goc nay o vi tri so le trong
=> AD// BC => ABCD la hinh thang

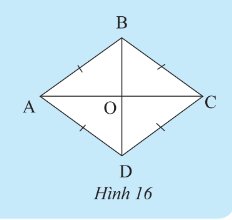
a) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(AD = BC\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta CDA\) (c-c-c)
\( \Rightarrow \widehat {BAC} = \widehat {ACD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\)
Chứng minh tương tự \(\Delta ADB = \Delta CBD\) (c-c-c)
\( \Rightarrow \widehat {ABD} = \widehat {CDB}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
\( \Rightarrow AD\;{\rm{//}}\;BC\)
b) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (do \(AB\) // \(CD\))
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)
\( \Rightarrow \widehat {BCA} = \widehat {CAD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AD\;{\rm{//}}\;BC\)
c) Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(BC = AD\) (gt)
\(\widehat {{\rm{BCA}}} = \widehat {{\rm{CDA}}}\) (do \(AD\) // \(BC\))
\(AC\) chung
Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c)
Suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra: \(AB\) // \(CD\)
d) Xét tứ giác \(ABCD\) ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Mà \(\widehat A = \widehat C\); \(\widehat B = \widehat D\) (gt)
Suy ra \(\widehat A + \widehat D = 180^\circ ;\;\widehat A + \widehat B = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(AB\;{\rm{//}}\;CD;\;AD\;{\rm{//}}\;BC\)
e) Xét \(\Delta APB\) và \(\Delta CPD\) ta có:
\(PA = PC\) (gt)
\(\widehat {{\rm{APB}}} = \widehat {{\rm{CPD}}}\) (đối đỉnh)
\(PB = PD\) (gt)
Suy ra: \(\Delta APB = \Delta CPD\) (c-g-c)
Suy ra: \(\widehat {BAP} = \widehat {PCD}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\;{\rm{//}}\;CD\)
Chứng minh tương tự: \(\Delta APD = \Delta CPB\) (c-g-c)
Suy ra \(\widehat {{\rm{DAP}}} = \widehat {{\rm{BCP}}}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AD\) // \(BC\)

Bài 1:
a.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = 1800 - D = 1800 - 540 = 1260
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 - C = 1800 - 1050 = 750
b.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = (1800 - 320) : 2 = 740
=> D = 1800 - 740 = 1060
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 : (1 + 2) . 2 = 1200
=> C = 1800 - 1200 = 600
Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

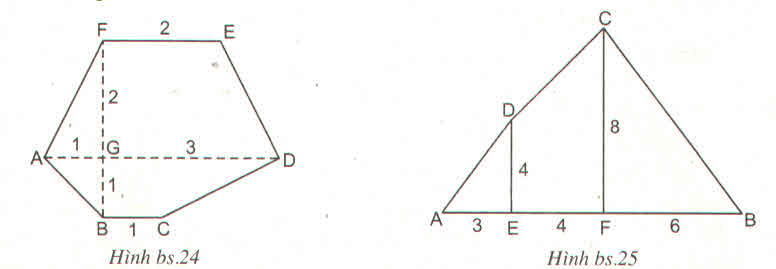
Bài giải:
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)