Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ∠(ADC) = ∠(BCD) (gt)
⇒ ∠(ODC) = ∠(OCD)
⇒ΔOCD cân tại O (dhnb tam giác cân)
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (hình thang ABCD cân)
⇒ OA = OB
Xét ΔADC và. ΔBCD:
AD = BC (hình thang ABCD cân )
AC = BD (hình thang ABCD cân)
CD chung
Do đó ΔADC và ΔBCD (c.c.c)
⇒ ∠D1= ∠C1
⇒ΔEDC cân tại E (dhnb tam giác cân)
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (hình thang ABCD cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
Mà OA = OB (cmt)
Nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.

1.
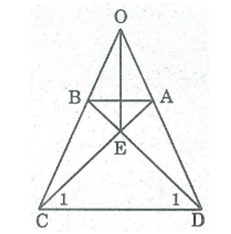
O A B D C E
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.