TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 9 2021
Bổ sung đề : ABCD là hthang cân
a) Ta có:
ABCD là hthang cân
=> \(\widehat{BAD}=\widehat{ABC}\)
\(\Rightarrow180^0-\widehat{BAD}=180^0-\widehat{ABC}\)
\(\Rightarrow\widehat{OAB}=\widehat{OBA}\)
=> Tam giác AOB cân tại O
b) Xét ΔABD và ΔBAC có:
AD=BC(ABCD là hthang cân)
\(\widehat{BAD}=\widehat{ABC}\)(ABCD là hthang cân)
AB chung
=> ΔABD=ΔBAC(c.g.c)
c) Ta có: ΔABD=ΔBAC(cmt)
=> \(\widehat{EDC}=\widehat{ECD}\)
=> Tam giác EDC cân tại E
=>EC=ED
25 tháng 8 2021
Bài 6:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
25 tháng 8 2021
Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
25 tháng 8 2021
Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK và HB=KC
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{HC}\)
Do đó: KH//BC
Xét tứ gác BKHC có KH//BC
nên BKHC là hình thang
mà KC=BH
nên BKHC là hình thang cân
25 tháng 8 2021
Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{AC}\)
Do đó: HK//BC
Xét tứ giác BCHK có HK//BC
nên BCHK là hình thang
mà HB=KC(ΔAHB=ΔAKC)
nên BCHK là hình thang cân
25 tháng 8 2021
Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
17 tháng 8 2023
Xét hình thang ABCD ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
mà \(\left\{{}\begin{matrix}\widehat{B}+\widehat{D}=180^o\left(đề.bài\right)\\\widehat{B}+\widehat{A}=180^o\left(t/c.hình.thang\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{C}=\widehat{D}\)
⇒ ABCD là hình thang cân (dpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 8 2023
Ta có : AB // CD ⇒ \(\widehat{B}\) + \(\widehat{C}\) = 180o mà \(\widehat{B}+\widehat{D}=\) 180o ⇒ \(\widehat{D}=\widehat{C}\)
Vì AB // CD; \(\widehat{D}=\widehat{C}\) vậy ABCD là hình thang cân
27 tháng 8 2021
a: Xét ΔABD có AB=AD
nên ΔABD cân tại A
Suy ra: \(\widehat{ABD}=\widehat{ADB}\)
mà \(\widehat{ABD}=\widehat{BDC}\)
nên \(\widehat{ADB}=\widehat{CDB}\)
hay DB là tia phân giác của \(\widehat{ADC}\)
PT
1
CM
22 tháng 10 2018
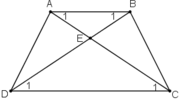
Gọi E là giao điểm của AC và BD.
+ 
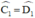⇒ ΔEDC cân tại E ⇒ ED = EC (1)
+ AB//CD ⇒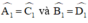 
(Các cặp góc so le trong)
Mà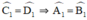 
⇒ ΔEAB cân tại E ⇒ EA = EB (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED hay AC = BD.
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
28 tháng 8 2022
Câu 1:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
Suy ra: DE=CF
Bài 2:
b: Xét ΔBAD và ΔABC có
AB chung
AD=BC
BD=AC
Do đó: ΔBAD=ΔABC
Suy ra: góc EAB=góc EBA
=>ΔEAB cân tại E
=>EA=EB
11 tháng 7 2021
Vì \(AB//CD\Rightarrow\hept{\begin{cases}\widehat{OAB}=\widehat{ODC}\\\widehat{OBA}=\widehat{OCD}\end{cases}}\)(đồng vị)
Vì \(OA=OB\Rightarrow\Delta OAB\)cân tại O
\(\Rightarrow\widehat{OAB}=\widehat{OBA}\)
\(\Rightarrow\widehat{ODC}=\widehat{OCD}\)
Xét hình thang ABCD ,có:
\(\widehat{OCD}=\widehat{ODC}\)
\(\Rightarrow ABCD\)là hình thang cân
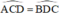
Tứ giác ABCD là hình thang có : AC =BD(gt)
\(\Rightarrow\)Tứ giác ABCD là hình thang cân
- Bạn đọc lại dấu hiệu nhận biết hình thang cân nhé
- Chúc bạn học tốt!!!