FB
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
XO
4 tháng 6 2021
Ta có a + b + c = 6
=> (a + b + c)2 = 36
=> a2 + b2 + c2 + 2ab + 2bc + 2ca = 36
=> 12 + 2ab + 2bc + 2ca = 36
=> 2ab + 2bc + 2ca = 24
=> ab + bc + ca = 12
Khi đó a2 + b2 + c2 = ab + bc + ca (= 12)
<=> 2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ca
<=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca = 0
<=> (a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ca + a2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
<=> \(\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\Leftrightarrow a=b=c\)
=> a = b = c = 2
Khi đó A = (2 - 3)2021 + (2 - 3)2021 + (2 - 3)2021
= -1 + (-1) + (-1)
= -3
LT
Cho a,b,c thõa mãn : a^2 + b^2 +c^2 - ab -bc- ca = 0. Tính: P = (a-b)^2020 + (b-c)^2021 + (c-a)^2022
1
TG
21 tháng 4 2021
\(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\) (1)
Mà: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\ge0\)
Nên PT (1) \(\Leftrightarrow\left\{{}\begin{matrix}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\\\left(a-c\right)^2=0\end{matrix}\right.\)
=> a = b = c
\(P=\left(a-b\right)^{2020}+\left(b-c\right)^{2021}+\left(c-a\right)^{2022}\)
\(=\left(a-a\right)^{2020}+\left(b-b\right)^{2021}+\left(c-c\right)^{2022}\)
= 0
LT
1 tháng 8 2023
a) A=x^2+4x+4=(x+2)^2.
Giờ ta tính giá trị của đa thức A với x=98:
A=(98+2)^2=100^2=10000
b) B=x^3+9x^2+27x+27=(x+3)^3.
Thế x=-103 => (-103+3)^3=-1000000
c) Tách C = a⋅b−a⋅c+2⋅c−2⋅b rồi kết hợp lại thành C=(a−2)⋅b+(2−a)⋅c.
Thế a,b,c vào được vậy
C=(2−2)⋅1.007+(2−2)⋅(−0.006) =0
d) Bài này khó quá mà tui nghĩ là đưa mấy cặp (2023^2-2022^2) thành dạng a^2-b^2=(a-b)(a+b) á
1 tháng 8 2023
d: D=(2023^2-2022^2)+(2021^2-2020^2)+...+(3^2-2^2)+(1^2-0^2)
=2023+2022+...+3+2+1+0
=2023*2024/2=2047276
HN
24 tháng 12 2021
Ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\frac{ab+bc+ca}{abc}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\left(ab+bc+ca\right)\left(a+b+c\right)=abc\)
\(\Leftrightarrow a^2b+ab^2+c^2a+ca^2+b^2c+bc^2+2abc=0\)
\(\Leftrightarrow\left(a^2+2ab+b^2\right)c+ab\left(a+b\right)+c^2\left(a+b\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(ab+bc+ca+c^2\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
=> Hoặc a+b=0 hoặc b+c=0 hoặc c+a=0
=> Hoặc a=-b hoặc b=-c hoặc c=-a
Ko mất tổng quát, g/s a=-b
a) Ta có: vì a=-b thay vào ta được:
\(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=-\frac{1}{b^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{1}{c^3}\)
\(\frac{1}{a^3+b^3+c^3}=\frac{1}{-b^3+b^3+c^3}=\frac{1}{c^3}\)
=> đpcm
b) Ta có: \(a+b+c=1\Leftrightarrow-b+b+c=1\Rightarrow c=1\)
=> \(P=-\frac{1}{b^{2021}}+\frac{1}{b^{2021}}+\frac{1}{c^{2021}}=\frac{1}{1^{2021}}=1\)
DT
25 tháng 2 2022
oh no bài thứ nhất là dạng chứng minh cs đúng ko ,
ko thể nào là dạng tìm a,b,c đc-.-
24 tháng 12 2021
Ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\frac{ab+bc+ca}{abc}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\left(ab+bc+ca\right)\left(a+b+c\right)=abc\)
\(\Leftrightarrow a^2b+ab^2+c^2a+ca^2+b^2c+bc^2+2abc=0\)
\(\Leftrightarrow\left(a^2+2ab+b^2\right)c+ab\left(a+b\right)+c^2\left(a+b\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(ab+bc+ca+c^2\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
=> Hoặc a+b=0 hoặc b+c=0 hoặc c+a=0
=> Hoặc a=-b hoặc b=-c hoặc c=-a
Ko mất tổng quát, g/s a=-b
a) Ta có: vì a=-b thay vào ta được:
\(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=-\frac{1}{b^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{1}{c^3}\)
\(\frac{1}{a^3+b^3+c^3}=\frac{1}{-b^3+b^3+c^3}=\frac{1}{c^3}\)
=> đpcm
b) Ta có: \(a+b+c=1\Leftrightarrow-b+b+c=1\Rightarrow c=1\)
=> \(P=-\frac{1}{b^{2021}}+\frac{1}{b^{2021}}+\frac{1}{c^{2021}}=\frac{1}{1^{2021}}=1\)
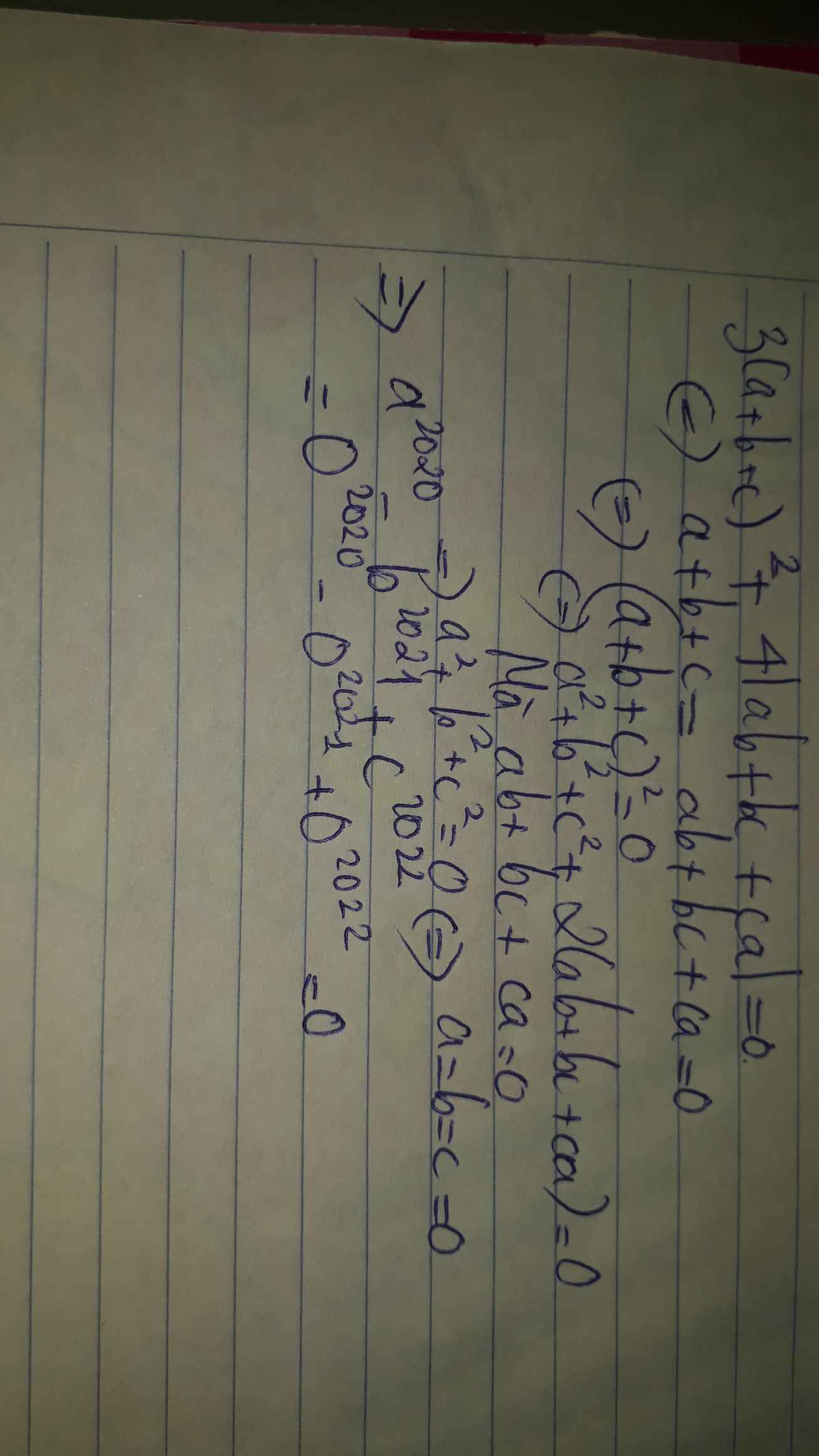
\(a+b+c=1\Leftrightarrow a+b=1-c\Leftrightarrow\left(a+b\right)^3=\left(1-c\right)^3\)
\(\Leftrightarrow a^3+b^3+3ab\left(a+b\right)=1-c^3-3c\left(1-c\right)\)
\(\Leftrightarrow3ab\left(a+b\right)=-3c\left(1-c\right)\)(vì \(a^3+b^3+c^3=1\))
\(\Leftrightarrow\left(a+b\right)\left(ab+c\right)=0\)(vì \(a+b=1-c\))
\(\Leftrightarrow\orbr{\begin{cases}a+b=0\\ab+c=0\end{cases}}\)
- \(a+b=0\Rightarrow c=1\Rightarrow a=b=0\).
- \(ab+c=0\):
Suy ra \(a+b-ab-1=0\Leftrightarrow\left(a-1\right)\left(b-1\right)=0\Leftrightarrow\orbr{\begin{cases}a=1\\b=1\end{cases}}\)
+) \(a=1\Rightarrow b=c=0\)
+) \(b=1\Rightarrow a=c=0\)
Vậy \(\left(a,b,c\right)=\left(1,0,0\right)\)và các hoán vị.
Khi đó \(P=1\).