Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: \(=\dfrac{1}{mn^2}\cdot\dfrac{n^2\cdot\left(-m\right)}{\sqrt{5}}=\dfrac{-\sqrt{5}}{5}\)
b: \(=\dfrac{m^2}{\left|2m-3\right|}=\dfrac{m^2}{3-2m}\)
c: \(=\left(\sqrt{a}+1\right):\dfrac{\left(a-1\right)^2}{\left(1-\sqrt{a}\right)}=\dfrac{-\left(a-1\right)}{\left(a-1\right)^2}=\dfrac{-1}{a-1}\)

b) \(\dfrac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\dfrac{2b}{a-b}\)
\(=\dfrac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\dfrac{2b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)-\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)-2b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{a+\sqrt{ab}-\sqrt{ab}+b-\sqrt{ab}+b-2b}{a-b}\)
\(=\dfrac{a}{a-b}\)

Áp dụng bđt cosi cho 3 số dương a,b,c>0
\(a+b+c\ge3\sqrt[3]{abc}\)
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3\sqrt[3]{\dfrac{1}{a}.\dfrac{1}{b}.\dfrac{1}{c}}\)
Suy ra\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\dfrac{1}{a}.\dfrac{1}{b}.\dfrac{1}{c}}=9\sqrt[3]{\dfrac{abc}{abc}}=9\)
Vậy \(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge9\)

a) CM:\(\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)^2-n^2\)
\(\Leftrightarrow n+1+n=\left(n+1-n\right)\left(n+1+n\right)\)
\(\Leftrightarrow2n+1=1\left(2n+1\right)\)
\(\Leftrightarrow2n+1=2n+1\)
\(\Rightarrow\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)^2-n^2\)
Câu b) ý 2:
Áp dụng BĐT cô si ta có :
\(\dfrac{a}{b}+\dfrac{b}{c}\ge2\sqrt{\dfrac{a}{c}}\\ \dfrac{b}{c}+\dfrac{c}{a}\ge2\sqrt{\dfrac{b}{a}}\\ \dfrac{c}{a}+\dfrac{a}{b}\ge2\sqrt{\dfrac{c}{b}}\\ \Leftrightarrow2\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)\ge2\left(\sqrt{\dfrac{a}{c}}+\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{c}{b}}\right)\\ \Rightarrowđpcm\)

\(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=a+b+c+2\left(\sqrt{ab}+\sqrt{ac}+\sqrt{bc}\right)=4\)
\(\Leftrightarrow\sqrt{ab}+\sqrt{ac}+\sqrt{bc}=1\)
\(\Rightarrow a+1=a+\sqrt{ab}+\sqrt{ac}+\sqrt{bc}=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\)
Tương tự: \(b+1=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\)
\(c+1=\left(\sqrt{a}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{c}\right)\)
\(VT=\sum\dfrac{\sqrt{a}}{a+1}=\sum\dfrac{\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)}\)
\(=\dfrac{\sqrt{a}\left(\sqrt{b}+\sqrt{c}\right)+\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)+\sqrt{c}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{c}\right)}\)
\(=\dfrac{2\left(\sqrt{ab}+\sqrt{ac}+\sqrt{bc}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{c}\right)}=\dfrac{2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{c}\right)}\)
\(VP=\dfrac{2}{\sqrt{\left(a+1\right)\left(b+1\right)\left(c+1\right)}}=\dfrac{2}{\sqrt{\left(\sqrt{a}+\sqrt{b}\right)^2\left(\sqrt{a}+\sqrt{c}\right)^2\left(\sqrt{b}+\sqrt{c}\right)^2}}\)
\(=\dfrac{2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{c}\right)}\)
\(\Rightarrow VT=VP\) (đpcm)

Lời giải:
Đặt \((\sqrt{a}; \sqrt{b}; \sqrt{c})=(x,y,z)\)
Khi đó điều kiện của bài toán trở thành:
\(x^2+y^2+z^2=x+y+z=2\Rightarrow xy+yz+xz=\frac{(x+y+z)^2-(x^2+y^2+z^2)}{2}=\frac{2^2-2}{2}=1\)
Ta có:
\(\frac{\sqrt{a}}{a+1}+\frac{\sqrt{b}}{b+1}+\frac{\sqrt{c}}{c+1}=\frac{x}{x^2+xy+yz+xz}+\frac{y}{y^2+xy+yz+xz}+\frac{z}{z^2+xy+yz+xz}\)
\(=\frac{x}{x(x+y)+z(x+y)}+\frac{y}{y(y+x)+z(y+x)}+\frac{z}{z(z+y)+x(y+z)}\)
\(=\frac{x}{(x+y)(x+z)}+\frac{y}{(y+x)(y+z)}+\frac{z}{(z+x)(z+y)}\)
\(=\frac{x(y+z)+y(x+z)+z(x+y)}{(x+y)(y+z)(x+z)}=\frac{2(xy+yz+xz)}{(x+y)(y+z)(x+z)}=\frac{2}{(x+y)(y+z)(x+z)}(*)\)
Và:
\(\frac{2}{\sqrt{(a+1)(b+1)(c+1)}}=\frac{2}{\sqrt{(x^2+1)(y^2+1)(z^2+1)}}\)
\(=\frac{2}{\sqrt{(x^2+xy+yz+xz)(y^2+xy+yz+xz)(z^2+xy+yz+xz)}}=\frac{2}{\sqrt{(x+y)(x+z)(y+z)(y+x)(z+x)(z+y)}}\)
\(=\frac{2}{\sqrt{(x+y)^2(y+z)^2(z+x)^2}}=\frac{2}{(x+y)(y+z)(x+z)}(**)\)
Từ \((*);(**)\Rightarrow \) đpcm.


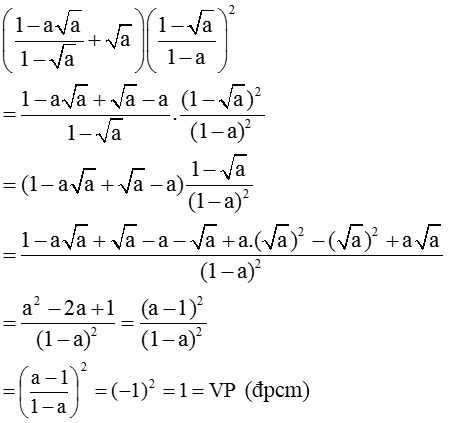
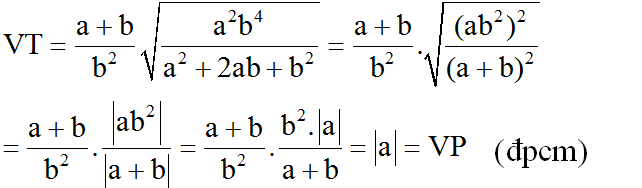
Ta có:
\(VT=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)-2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2-2\left(\dfrac{c}{abc}+\dfrac{a}{abc}+\dfrac{b}{bca}\right)}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2-2\left(\dfrac{a+b+c}{abc}\right)}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}\)
\(=\left|\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right|\)
\(\Rightarrow VT=VP\)
Vậy \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}=\left|\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right|\) (Đpcm)