Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do HC -HB = AB
Mà HC +HB =BC => nhân 2 vế ta có:
HC2 -HB2 =AB.BC (1).
Áp dụng định lí Pi-ta-go ta có:
HC2 =AC2-AH2
HB2 = AB2 -AH2
Nên HC2 - HB2 =AC2 -AB2 = (BC2 -AB2 ) -AB2 = BC2 -2AB2 ,(2).
Từ (1 ) và (2 ) có: BC2 - 2AB2 =AB.BC
<=> BC2 -AB.BC - 2AB2 = 0
<=> (BC +AB) (BC -2AB ) = 0,
Do AB +BC >0 nên BC = 2AB.
HC -HB = AB, HC +HB =BC
nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1).
Áp dụng Pitago ta có HC ^2 =AC^2-AH^2, HB^2 = AB^2 -AH^2 nên HC^2 - HB^2 =AC^2 -AB^2 = (BC^2 -AB^2 ) -AB^2 = BC^2 -2AB^2 ,(2). Từ (1 ) và (2 ) có BC^2 - 2AB^2 =AB.BC
<=> BC^2 -AB.BC - 2AB^2 = 0
<=> (BC +AB) (BC -2AB ) = 0,
do AB +BC >0 => BC - 2AB = 0 => BC = 2AB.
:3

a: Xét ΔAHB vuông tại H và ΔAHK vuông tại H có
AH chung
HB=HK
Do đó: ΔAHB=ΔAHK
=>\(\hat{BAH}=\hat{KAH}\)
=>AH là phân giác của góc BAK
c: Xét ΔABD vuông tại A có AB=AD
nên ΔABD vuông cân tại A
=>\(\hat{ABD}=\hat{ADB}=45^0\)
Xét tứ giác ABDE có \(\hat{BED}=\hat{BAD}=90^0\)
nên ABDE là tứ giác nội tiếp
=>\(\hat{ABD}+\hat{AED}=180^0\)
=>\(\hat{AED}=180^0-45^0=135^0\)

theo đề bài ta có BC=BH+HC mà HC-HB=AB nên ta có BC=HB+HC=2(HC-HB) nên ta có BC=2AB

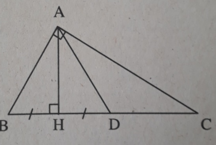
Trên HC lấy D sao cho HD = HB. Tam giác ABD có đường cao AH là trung tuyến nên là tam giác cân, suy ra
∠(ADB) = ∠B . (1)
Ta có: DC = HC – HD = HC – HB = AB = AD ( vì tam giác ABD cân tại A)
Nên ΔADC cân tại D, do đó ∠(DAC) = ∠C (2)
Ta có; ∠ADB + ∠DAC = ∠BAC = 90º (3)
Và ∠B + ∠C = 90º vì tam giác ABC vuông tại A (4)
Từ (2); (3) và (4) suy ra ∠(DAB) = ∠B . (5)
Từ (1) và (5) suy ra ∠(ADB) = ∠B = ∠(DAB) , do đó ΔABD là tam giác đều.
Suy ra AB = BD = AD = DC. Vậy BC = 2AB.

A B C H E F
a, Xét hai tam giác vuông ABH và tam giác vuông ACH có :
góc AHB = góc AHC = 90độ
AB = AC ( vì tam giác ABC cân tại A )
cạnh AH chung
Do đó : tam giác ABH = tam giác ACH ( cạnh huyền - cạnh góc vuông )
=> HB = HC ( cạnh tương ứng )
và góc BAH = góc CAH ( góc tương ứng )
b,Xét tam giác AHE và tam giác AHF có :
góc AEH = góc AFH = 90độ
cạnh AH chung
góc HAE = góc HAF ( theo câu a )
Do đó ; tam giác AHE = tam giác AHF ( cạnh huyền - góc nhọn )
=> AE = AF ( cạnh tương ứng )
=> tam giác AEF cân tại A
=> góc AEF = góc AFE = \(\frac{180^0-\widehat{A}}{2}\) ( 1 )
Vì tam giác ABC là tam giác cân nên :
góc ABC = góc ACB = \(\frac{180^0-\widehat{A}}{2}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : góc AEF = góc AFE = góc ABC = góc ACB
mà góc AEF = góc ABC và ở vị trí đồng vị
=> EF // BC .
Học tốt