Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


nếu bạn ko thấy ảnh thì zô thống kê hỏi đáp của mình là thấy bài này nhá . ( cậu tìm câu nào có câu này r ấn zô xem nha )
hoặc link bài của mình nè
https://scontent-hkt1-1.xx.fbcdn.net/v/t1.15752-9/89947717_345887062999332_7304147707155709952_n.jpg?_nc_cat=110&_nc_sid=b96e70&_nc_ohc=Hj57duZ44dcAX91P2ra&_nc_ht=scontent-hkt1-1.xx&oh=7ea184f17776bd230198145c38f92aae&oe=5E95F1D5

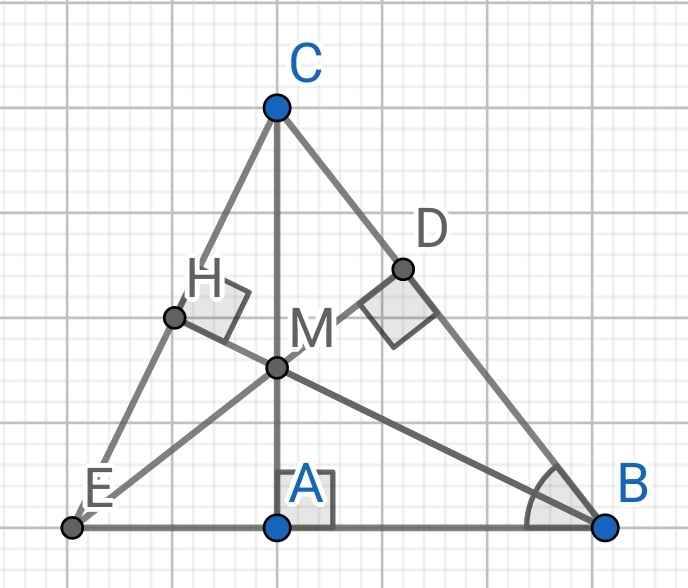 a) Do BM là tia phân giác của ABC (gt)
a) Do BM là tia phân giác của ABC (gt)
⇒ ∠ABM = ∠DBM
Xét hai tam giác vuông: ∆ABM và ∆DBM có:
BM là cạnh chung
∠ABM = ∠DBM (cmt)
⇒ ∆ABM = ∆DBM (cạnh huyền - góc nhọn)
⇒ BA = BD (hai cạnh tương ứng)
b) Xét hai tam giác vuông: ∆ABC và ∆DBE có:
BA = BD (cmt)
∠B chung
⇒ ∆ABC = ∆DBE (cạnh huyền - góc nhọn)
c) Do ∠ABM = ∠DBM (cmt)
⇒ ∠EBM = ∠CBM
Do ∆ABC = ∆DBE (cmt)
⇒ BC = BE (hai cạnh tương ứng)
Xét ∆MBE và ∆MBC có:
BE = BC (cmt)
∠EBM = ∠CBM (cmt)
BM là cạnh chung
⇒ ∆MBE = ∆MBC (c-g-c)
⇒ ME = MC (hai cạnh tương ứng)
c) ∆BCE có:
CA ⊥ AB (ABC vuông tại A)
⇒ CA ⊥ BE
⇒ CA là đường cao của ∆BCE (1)
MD ⊥ BC (gt)
⇒ ED ⊥ BC
⇒ ED là đường cao thứ hai của ∆BCE (2)
M là giao điểm của AC và ED
⇒ M là giao điểm của ba đường cao của ∆BCE
Mà BH ⊥ CE (gt)
⇒ BH là đường cao thứ ba của ∆BCE
⇒ B, M, H thẳng hàng

Hình tự vẽ
a, \(\Delta BAM\)và \(\Delta BDM\)có
\(\widehat{ABM}=\widehat{DBM}\left(gt\right)\)
\(AM\): cạnh chung
\(\widehat{BAM}=\widehat{BDM}\left(=90^o\right)\)
\(\Rightarrow\Delta BAM=\Delta BDM\left(ch-gn\right)\)
\(\Rightarrow BA=BD\)(2 cạnh tương ứng )
Để nghĩ tiếp :(
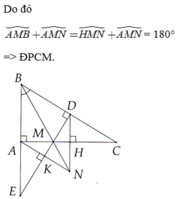
Ta có:
∠AMB+∠ABM=90o
∠BMD+∠MBD=900
Mà ∠AMB=∠BMD (gt)
=> ∠ABM=∠MBD
Xét ΔBAM và ΔBAM có:
∠ABM=∠MBD (gt)
BM chung
∠ABM=∠MBD (cmt)
=> ΔBAM = ΔBAM (g-c-g)
=> BA=BD (2 cạnh tương ứng)
b,Xét ΔABC và ΔDBE có:
∠ABC chung
∠BAC=∠BDM=90o
BA=BD (cmt)
=> ΔABC = ΔDBE (g-c-g)
c,Ta có
BC⊥ED
AK⊥ED
=> BC//AK hay BC//AN
=> ∠ANM=∠MBC ( 2 góc slt) (1)
Mà:
DH⊥AC
BA⊥AC
=> BA//DH hay BA//DN
=> ∠MND=∠ABM ( 2 góc so le trong) (2)
Mà ∠ABM=∠MBD ( vì BM là tia phân giác của góc ABC)
Từ(1) và (2) =>∠ANM=∠MND
=> NM là tia phân giác của góc HMK
d,Ta có BM là tia phân giác của góc ABC (3)
Và NM là tia phân giác của góc HMK
Vì ∠ANM=∠MBC
∠MND=∠ABM
=> ∠ANM=∠MBC=∠MND=∠ABM
=> BN là tia phân giác của góc ABC (4)
Từ (3) và (4) => B,M,N thẳng hàng

a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó:ΔBAM=ΔBDM
Suy ra:BA=BD
b: Xét ΔBDE vuông tại D và ΔBAC vuông tại A có
BD=BA
\(\widehat{DBE}\) chung
Do đó: ΔBDE=ΔBAC

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
b: ΔBAM=ΔBDM
=>BA=BD và MA=MD
Xét ΔMAE vuông tại A và ΔMDC vuông tại D có
MA=MD
\(\widehat{AME}=\widehat{DMC}\)
Do đó: ΔMAE=ΔMDC
=>ME=MC
c: ΔMAE=ΔMDC
=>AE=DC
BA+AE=BE
BD+DC=BC
mà BA=BD
và AE=DC
nên BE=BC
Xét ΔABC vuông tại A và ΔDBE vuông tại D có
BC=BE
BA=BD
Do đó: ΔABC=ΔDBE
Ta có: BE=BC
=>B nằm trên đường trung trực của EC(1)
Ta có: ME=MC
=>M nằm trên đường trung trực của EC(2)
Xét ΔBEC có BE=BC
nên ΔBEC cân tại B
Ta có: ΔBEC cân tại B
mà BH là đường cao
nên BH là trung trực của EC(3)
Từ (1),(2),(3) suy ra B,M,H thẳng hàng