
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

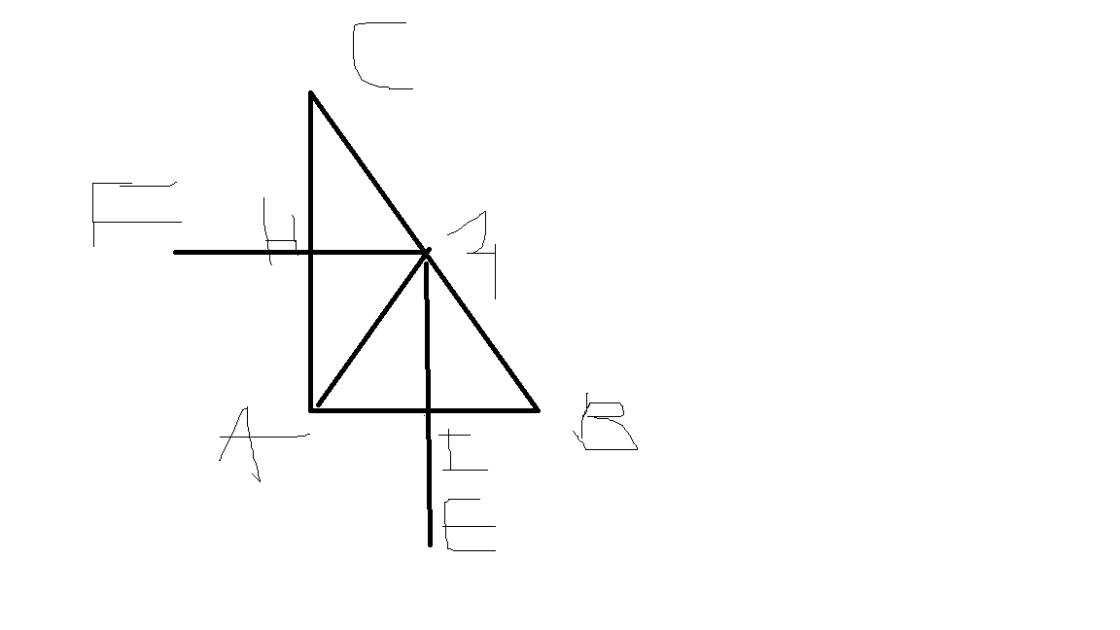

a: E đối xứng M qua AB
nên AB là trung trực của ME
=>AB vuông góc với ME tại trung điểm của ME
=>AB là phân giác của góc EAM(1)
E đối xứng N qua AC
nên AC là trung trực của NE
=>AC vuông góc với NE tại trung điểm của NE
=>AC là phân giác của góc EAN(2)
Xét tứ giác AIEK có
góc AIE=góc AKE=góc KAI=90 độ
nên AIEK làhình chữ nhật
b: Từ (1), (2) suy ra góc NAM=2*90=180 độ
=>N,A,M thẳng hàng
mà AM=AN
nên A là trung điểm của MN

Sửa đề: K là điểm đối xứng của M qua AC
a: M đối xứng H qua AB
=>AB là đường trung trực của MH
=>AB vuông góc MH tại trung điểm của MH
=>AB vuông góc MH tại E và E là trung điểm của MH
M đối xứng K qua AC
=>AC là đường trung trực của MK
=>AC vuông góc với MK tại trung điểm của MK
=>AC vuông góc với MK tại F và F là trung điểm của MK
ME\(\perp\)AB
AC\(\perp\)AB
Do đó: ME//AC
MF\(\perp\)AC
AB\(\perp\)AC
Do đó: MF//AB
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật
Xét tứ giác AMBH có
E là trung điểm của AB và MH
Do đó: AMBH là hình bình hành
Hình bình hành AMBH có MH\(\perp\)AB
nên AMBH là hình thoi
Xét tứ giác AMCK có
F là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có AC\(\perp\)MK
nên AMCK là hình thoi
b: AMBH là hình thoi
=>AB là phân giác của góc MAH
=>\(\widehat{MAH}=2\cdot\widehat{BAM}\)
AMCK là hình thoi
=>AC là phân giác của góc MAK
=>\(\widehat{MAK}=2\cdot\widehat{MAC}\)
\(\widehat{MAH}+\widehat{MAK}=\widehat{KAH}\)
=>\(\widehat{KAH}=2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)\)
=>\(\widehat{KAH}=2\cdot90^0=180^0\)
Do đó: K,A,H thẳng hàng
mà AH=AK(=AM)
nên A là trung điểm của HK
c: Để hình chữ nhật AEMF trở thành hình vuông thì AE=AF
mà \(AE=\dfrac{AB}{2};AF=\dfrac{AC}{2}\)
nên AB=AC

a: Ta có: H và M đối xứng nhau qua AB
nên AB là đường trung trực của HM
Suy ra: AB\(\perp\)HM và E là trung điểm của HM
Ta có: M và K đối xứng nhau qua AC
nên AC là đường trung trực của MK
Suy ra: AC\(\perp\)MK và F là trung điểm của MK
Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{EAF}=90^0\)
Do đó: AEMF là hình chữ nhật
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Xét tứ giác AMBH có
E là trung điểm của đường chéo MH
E là trung điểm của đường chéo AB
Do đó: AMBH là hình bình hành
mà MH\(\perp\)AB
nên AMBH là hình thoi
Xét tứ giác AMCK có
F là trung điểm của đường chéo MK
F là trung điểm của đường chéo AC
Do đó: AMCK là hình bình hành
mà AC\(\perp\)MK
nên AMCK là hình thoi

a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật

a: M đối xứng E qua AB
=>AB là đường trung trực của ME
=>AB\(\perp\)ME tại I và I là trung điểm của ME
Ta có: M đối xứng F qua AC
=>AC là đường trung trực của MF
=>AC\(\perp\)MF tại K và K là trung điểm của MF
Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
=>AIMK là hình chữ nhật
b: Ta có: AKMI là hình chữ nhật
=>AK//MI và AK=MI; KM//AI và KM=AI
Ta có: MI//AK
I\(\in\)ME
Do đó: IE//AK
Ta có: AK=IM
IM=IE
Do đó: AK=IE
Ta có: AI=MK
MK=KF
Do đó: AI=KF
Ta có: AI//MK
K\(\in\)MF
Do đó: AI//KF
Xét tứ giác AKIE có
AK//IE
AK=IE
Do đó: AKIE là hình bình hành
=>KI//AE và KI=AE
Xét tứ giác AIKF có
AI//KF
AI=KF
Do đó: AIKF là hình bình hành
=>KI//AF và KI=AF
Ta có: KI//AF
KI//AE
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
Ta có: KI=AE
KI=AF
Do đó: AE=AF
mà E,A,F thẳng hàng
nên A là trung điểm của EF